Алгебра и теория чисел

1.

а) На множестве Z бинарное отношение задано правилом: x G y 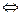x 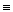y (mod 5). Доказать, что G – отношение эквивалентности. Постройте классы эквивалентности и фактор–множество .

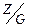б) На множестве R бинарное отношение задано правилом: x G y 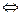x 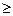y. Покажите, что G – отношение нестрогого линейного порядка на R.

в) Бинарное отношение G задано графом. Найдите D(G), E(G). Является ли G отношением эквивалентности?

b

а d

с

2.

а) Докажите, что всякая группа с тремя элементами является абелевой.

б) Докажите, что множество М невырожденых матриц порядка n является группой относительно умножения.

в) Докажите, что множество А = {x | x = a + b 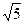, где a, b Î Q и a² + b² ¹0} является мультипликативной группой.

3.

а) Докажите, что множество К = {x | x = a + b 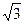, где a, b Î Q } относительно сложения и умножения действительных чисел является кольцом.

б) Докажите, что множество К = {x | x = a + b i, где a, b Î Z } относительно сложения и умножения комплексных чисел является кольцом.

в) Будет ли множество пар (a, b), где a, b Î Z кольцом относительно операций:

(a₁, b₁) + (a₂, b₂) = (a₁ + a₂, b₁ + b₂) и (a₁, b₁) × (a₂, b₂) = (a₁ × a₂, b₁ ×b₂)?

4. Доказать методом математической индукции:

а) " n Î N, (n ² + 5) × n 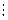6;

б) " n Î N, (10 ⁿ + 18 n –28) 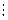27;

в) n ≥ 10 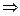2 ⁿ > n ³, " n Î N.

5. Найдите НОД и НОК чисел:

а) 91, 21, 39;

б) 91, 247;

в) 153, 63.

6.

а) Докажите, что кольцо классов вычетов по модулю 5 является полем.

б) Докажите, что Р = {x | x = a + b 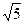, где a, b Î Q } относительно сложения и умножения действительных чисел является полем.

в) Используя свойства упорядоченного поля, докажите, что

а Î R, с₁, с₂, r Î N, а > 0, с₁ < r< с₂, 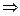(а^r 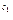– а 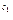) ≤ (а – а ).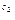

7. Вычислить:

а) (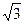 + i)¹²;

б) ;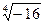

в) .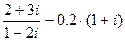

8. Исследовать на линейную зависимость систему векторов, найти ее базис и ранг:

а) 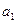= (1, –1, 2, 3), 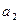= (1, 0, 2, –1), 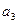= (–1, –2, –2, 9);

б) 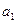= (1, 2, 3), 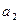= (4, 5, 6), 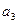= (7, 8, 9);

в) 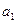= (1, 2, 1), 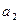= (2, –1, 2), 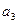= (–2, 0, 2).

9. Решите систему линейных уравнений:

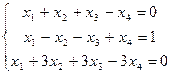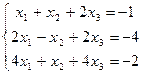а) ; б) ; в) .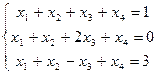

10.

а) Проверьте, является ли система векторов 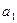= (2; 3; 0); 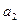= (0; 5; 6); 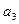= (7; 0; 8) базисом для R ³?

б) Векторное пространство порождено системой (1; 1; 0); (0; 2; 3); (3; 0; –1); (0; 5; 0) из R ³. Найдите базис и размерность этого пространства.

в) Найдите базис и размерность векторного пространства L = (L, +, R) над полем R, если L = {0, a, b, 0 | a, b Î R}.

11.

а) Составьте таблицу простых чисел, не превосходящих 40, методом решета Эратосфена. Решите и обоснуйте.

б) Являются ли числа 157 и 187 простыми?

в) Найдите каноническое разложение числа 8840.

12.

а) Является ли полной системой вычетов по модулю 6 система чисел: 15, –6, 2, 34, 25, –19?

б) Найдите остаток от деления 11⁸⁰² на 1000. Использовать теорему Эйлера.

в) Решите сравнение: 21x = 51 (mod 54).

13.

а) Докажите, что при любом нечетном числе n Î N верно (n ³ – n) 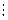24.

б) Найдите длину периода дроби 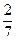в десятичной системе счисления. Результат проверьте вычислением.

в) Докажите, что остаток при делении квадрата целого числа на 4 равен 0 или 1.

14. Найдите НОД многочленов:

а) f (x) = x⁴ + 6x³ +17x² + 24x + 12; g (x) = x³ – 2x² – 13x – 10;

15. Разложите на неприводимые множители многочлен над полем R и над полем С:

а) f (х) = х⁴ + 4;

б) f (х) = х⁴ – 4;

в) f (х) = х⁴ + 3х² + 9.

16. Освободитесь от алгебраической иррациональности в знаменателе дроби:

а) ;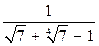

б) 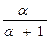, если a³ – 3a + 1 = 0;

в) .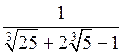

Дата добавления: 2015-07-12