Бесконечно малые и бесконечно большие функции

Определение 8. Функция a(x) называется бесконечно малой при x ® x ₀, или в точке , если предел a(x) при x® , равен нулю: .

Определение 9. Функция f (x) называется бесконечно большой в точке , если предел f (x) при x ® x ₀, равен ∞. Это значит, что для любого сколь угодно большого числа M > 0 существует малое число δ=δ(M) > 0 такое, что для любого 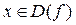, удовлетворяющего неравенству 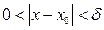, выполняется неравенство | f (x)| > M.

Определение 10. Функция f (x) называется ограниченной на некотором множестве X ÌD(f), если существует такое число M >0, что для любого x Î X, выполняется неравенство: .

Дата добавления: 2015-07-10