Основные свойства бесконечно малых функций

1) Алгебраическая сумма конечного числа бесконечно малых функций в точке есть бесконечно малая функция в этой точке . То есть: если - бесконечно малые функции в точке , то - бесконечно малая функция в этой точке .

2) Произведение конечного числа бесконечно малых функций в точке есть бесконечно малая функция в точке . То есть: если - бесконечно малые функции в точке , то 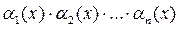- бесконечно малая функция в этой точке .

3) Произведение бесконечно малой функции в точке на ограниченную функцию в некоторой окрестности точки есть бесконечно малая функция в точке , то есть, если α(x) бесконечно малая функция в точке и f (x) ограниченная в некоторой окрестности точки , то α(x)× f (x) – бесконечно малая функция в точке .

Следствие из свойства 3). Произведение постоянной на бесконечно малую функцию в точке есть бесконечно малая функция в точке . То есть: если α(x) – бесконечно малая функция в точке , то с×α(x)- бесконечно малая функция в точке x ₀.

Теорема ( о связи между бесконечно малой функцией в точке и бесконечно большой в точке )

Если функция f (x ) является бесконечно большой в точке , то функция является бесконечно малой в точке .

( Верно и обратное утверждение)

Дата добавления: 2015-07-10