
Читайте также:
|
(слайды 3 и 4 в перезнтации)
Определение 6. Точка x 0 называется точкой устранимого разрыва функции f (x), если предел функции в этой точке существует, но f (x) в точке x 0 либо не определена, либо имеет значение f (x 0), не совпадающее с найденным пределом:
f (x 0-0)= f (x 0+0) ¹ f (x 0).
Определение 7. Точка x 0 называется точкой разрыва первого рода функции f (x) (разрыв типа «скачка»), если в этой точке функция имеет конечные, но не равные между собой правый и левый пределы, то есть:
f (x 0-0) ¹ f (x 0+0).
Определение 8. Точка x 0 называется точкой разрыва второго рода функции f (x), если в этой точке f (x) не имеет хотя бы одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
Примеры. Исследовать функции на непрерывность и точки разрыва.
1. 
Решение. На промежутке (-∞;-1) f (x)= - x +1, на (-1;1)  и на (1;+∞) f (x) = x -1.
и на (1;+∞) f (x) = x -1.
На этих промежутках f (x) элементарная функция, непрерывна при всех x, принадлежащих этим промежуткам. Необходимо проверить непрерывность в точках x = -1 и x =1.
1) 
2) 
Получили, что f (-1-0) ¹ f (-1+0) => x = -1 – точка разрыва f (x) I рода.
3) 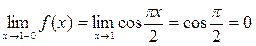
4) 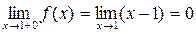
Получили, что f (1-0) = f (1+0) = f (1) = 0 => x = 1 – точка непрерывности функции f (x).
Ответ: f (x) непрерывна на (-∞;-1) и на (-1;+∞), точка x = -1 – точка разрыва I рода.
2. f (x) = 
Решение. На промежутках (-∞;0) и на (0;+∞) f (x) непрерывна. Исследуем точку x =0 Ï D(f).
1) 
2) 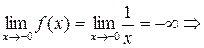
=> x =0 – точка разрыва f (x) II рода.
Дата добавления: 2015-07-10; просмотров: 147 | Нарушение авторских прав