Производные обратных тригонометрических функций

Теорема 10. Функция y = a rcsin x дифференцируема при любом x Î(-1;1) и справедлива формула:

Доказательство: Функция y = a rcsin x определена при x Î[-1;1] и область ее значений 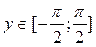. Она монотонно возрастает на всей области ее определения, поэтому имеет обратную функцию x = sin y. Уравнение x = sin y можно рассматривать как неявное задание функции y = a rcsin x. Найдем производную от обеих частей уравнения:

.

Выразим из полученного равенства y ':

.

Но 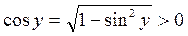при .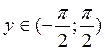

Поэтому , так как .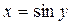

Следовательно, получаем:

.

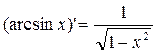Теорема 11. Функция y = arcos x дифференцируема при x Î (-1;1) и справедлива формула:

.

Теорема 12. Функция y = a rct gx дифференцируема при x Î (-¥:+¥) и справедлива формула:

.

Теорема 13. Функция y = a rcсt gx дифференцируема при x Î (-¥:+¥) и справедлива формула:

.

Теоремы 11, 12, и 13 доказываются аналогично доказательству теоремы 10.

Дата добавления: 2015-07-10