Правила дифференцирования

Теорема 3. Если функции U (x) и V (x) дифференцируемы в точке x, то функция U (x) ± V (x) дифференцируема в т. x и ее производная вычисляется по формуле:

(U (x) ± V (x))' = (U (x))' ± (V (x))'.

Доказательство: Рассмотрим функцию y = U (x) ± V (x).

Тогда D y =D U ±D V. Разделим на D x и перейдем к пределу при D x ®0:

так как по условию теоремы функции U (x) и V (x) дифференцируемы.

Значит, (U (x) ± V (x))' = U ' (x) ± V ' (x).

Теорема доказана.

Теорема 4. Если функции U (x) и V (x) дифференцируемы в т. х, то функция (U (x) × V (x)) дифференцируема в т. х и ее производная вычисляется по формуле:

(U (x) × V (x))' = (U (x))'× V (x) + U (x) × (V (x))'.

Доказательство. Рассмотрим функцию y = U (x)× V (x). Найдем ее приращение D y = (U +D U)(V +D V) - U × V = U × V + U ×D V + V ×D U + D U ×D V - U × V = = U ×D V + V ×D U + D U ×D V.

Разделим D y на D x и перейдем к пределу при D x ®0:

так по условию функции U (x) и V (x) дифференцируемы, а значит 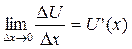, и .

Значит, (U (x)× V (x))' = U ’(x) × V (x) + U (x) × V ' (x).

Теорема доказана.

Дата добавления: 2015-07-10