Следствия.

а) Если U (x), V (x) и W (x) дифференцируемы в т. х, то функция (U (x) × V (x) × W (x)) дифференцируема в т. х и ее производная вычисляется по формуле:

(U × V × W)' = U '× V × W + U × V '× W + U × V × W '.

б) Производная постоянной, умноженной на дифференцируемую функцию, равна этой постоянной, умноженной на производную функции:

(C× U (x))' = C× U ' (x).

Теорема 5. Если функции U (x) и V (x) дифференцируемы в точке х и V (x)#0, то функция 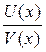дифференцируема в точке х и ее производная вычисляется по формуле: .

Доказательство. Рассмотрим функцию 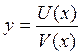. Найдем ее приращение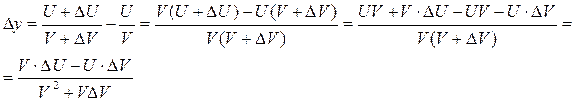

Разделим D y на D x и перейдем к пределу при D x ®0:

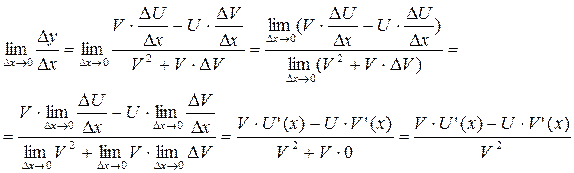
Значит, .

Теорема доказана.

Теорема 6 (производная сложной функции)

Если функция f (u) дифференцируема в точке u, а функция u (x) дифференцируема в точке x, причем u = u (x), тогда сложная функция f (u(x)) дифференцируема в точке x и ее производная вычисляется по формуле:

(f (u (x)))' = f '(u) × u ' (x).

Доказательство. Рассмотрим функцию y = f (U). Так как функция f (u) дифференцируема в точке u, то ее приращение можно записать в виде:

, где

Разделим на D x и перейдем к пределу при D x ®0:

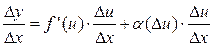
(если D x ®0, то D u ®0, т.к. u (x) дифференцируема, а значит непрерывна)

Значит: (f (u (x)))' = f ’(u) × u ' (x).

Теорема доказана.

Дата добавления: 2015-07-10