Дифференциал функции

Пусть функция y = f (x) дифференцируема в точке x, тогда ее приращение можно записать в виде двух слагаемых, первое из которых линейно относительно D x, а второе бесконечно малое при D x ®0 более высокого порядка малости по сравнению с D x:

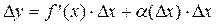, где a(D x) ® 0 при D x ® 0.

Определение 4. Слагаемое f ’(x)× D x называется главной линейной относительно D x частью приращения функции y = f (x), называемой дифференциалом этой функции. Дифференциал обозначается

dy = y ' (x)× D x.

Если x – независимая переменная, то справедливо равенство: D x = dx, так как (x)' = 1. Тогда формула для дифференциала записывается:

dy = y ' (x)× dx.

Так как второе слагаемое приращения функция – малая величина более высокого порядка малости по сравнению с D x, то между приращением функции и ее дифференциалом можно поставить приближенное равенство. Это равенство тем точнее, чем меньше D x. На основе этого приближенного равенства получается приближенное представление значения дифференцируемой функции (слайд 6 в презентации):

Пример. Вычислить приближенно

Решение. Рассмотрим функцию . В качестве начальной точки возьмем x ₀ = 4, приращение D x = 0,08, .

Подставим в формулу:

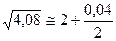
, где D<<0,08.

Дата добавления: 2015-07-10