Односторонние пределы

Определение 5. Число А называется правым (левым) пределом функции y = f (x) в точке x ₀, если для любого малого числа ε > 0 найдется другое малое число такое, что для всех и лежащих в правой (левой) окрестности точки x ₀, то есть (), справедливо неравенство: .

При этом используют следующие обозначения:

- для правого предела.

- для левого предела.

Замечание 1. Если f (x) имеет в точке x ₀ предел равный А, то существуют и 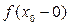и справедливо равенство:

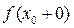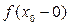= =А.

Замечание 2. Если f (x) имеет в точке x₀ правый и левый пределы, равные между собой, то в точке функция f (x) имеет предел равный числу:

А= = .

Замечание 3. Если f (x) имеет в точке x ₀ правый и левый пределы, но они не равны между собой, то в точке x ₀ функция f (x) не имеет предела.

Дата добавления: 2015-07-10