Элементарные функции

4.1 Основные элементарные функции:

y = (степенная функция), α ÎR, E(y), D(y) зависят от α.

y = (показательная функция), a^a > 0, a^a ≠ 1, D(y) = R, E(y) = (0;+∞).

y = (логарифмическая функция), a^a > 0, a^a ≠ 1, E(y) =R, D(y) = (0;+∞). y = const (постоянная функция). D(y) = R; E(y) = c.

Тригонометрические функции:

y = cos x, D(y) = R, E(y)= .

y = sin x, D(y) = R, E(y)= .

y = t gx, D(y) = , E(y) = R.

y = ct gx, D(y) = 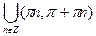, E(y) = R.

Обратные тригонометрические функции:

y = a rcsin x, D(y) = , E(y) = .

y = a rccos x, D(y) = , E(y) = .

y = a rct gx, D(y) = R, E(y) = .

y = a rcct gx, D(y) = R, E(y) = .

Графики обратных тригонометрических функций:

y = a rcsin x Рис. 1	y = a rccos x Рис. 2
y = a rct gx Рис. 3	y = a rcct gx Рис. 4

4.2 Элементарной функцией называется функция, составленная из основных элементарных функций с помощью конечного числа операций сложения, вычитания, умножения, деления и суперпозиции.

Например: - элементарная функция.

Дата добавления: 2015-07-10