Сложная и обратная функции

Определение 1. Пусть функция y = f (U) определена на множестве D(f), а функция U = g (x) определена на D(g), причем E(g) 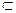D(f).

Тогда функция y = F (x) = f (g (x)) называется сложной функцией (сложная функция = функция f от функции g = суперпозиция функций f и g).

Определение 2. Пусть задана функция y = f (x), взаимно и однозначно отображающая множество X= D(f) на множество Y= E(f).

Тогда функция x = g (y) называется обратной к функции y = f (x).

То есть любому y E(f) соответствует единственное значение x D(f), при котором верно равенство y = f (x).

Дата добавления: 2015-07-10