Теоремы о конечных пределах

Теорема 1. Функция f (x) имеет конечный предел в точке тогда и только тогда, когда выполняется равенство: f (x)=А+ a(x), где a(x) – бесконечно малая функция в точке .

Доказательство этой теоремы вытекает из определения предела функции в точке и определения бесконечно малой функции в точке.

Теорема 2. Если существуют конечные пределы двух функций f (x) и g (x) в точке , то существует конечный предел суммы этих функций в точке , равный сумме пределов этих функций.

Доказательство: Пусть , тогда по теореме 1 f (x)= А + a(x), где a(x) – бесконечно малая функция в точке x ₀.

Пусть, , тогда по теореме 1 g (x)= B + β (x), где β (x) – бесконечно малая функция в точке x ₀. Рассмотрим сумму этих функций: f (x) + g (x) = = A + a(x) + B + β (x) = (A+B) + a(x) + β (x), обозначим γ (x) = a(x) + β (x) -

бесконечно малая функция в точке x ₀ ( по свойству 1 бесконечно малых функций). Получим f (x)+ g (x)= A+B +γ(x).

По теореме 1: .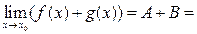

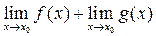Теорема доказана.

Теорема 3. Если существуют конечные пределы двух функций f (x) и g (x) в точке , то существуетпредел произведения этих функций в точке , равный произведению пределов этих функций.

Доказательство: Пусть 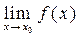= А, тогда по теореме 1: f (x)= А + a(x), где a(x) – бесконечно малая функция в точке . Пусть , тогда по теореме 1: g (x) = B + β (x), где β (x) – бесконечно малая функция в точке . Рассмотрим произведение этих функций:

f (x) × g (x) = (А + a(x))(B + β (x)) = AB + B × a(x) + A×β (x) + a(x) × β (x).

Обозначим: B × a(x) + Aβ (x) + a(x)β (x) = γ (x) – бесконечно малая функция в точке ( посвойствам бесконечно малых функций). Получим: f (x)× g (x) = A×B + γ (x).

По теореме 1: .

Теорема доказана.

Теорема 4. Если существуют конечные пределы f (x) и g (x), причем , то существует предел частного этих функций в точке , равный частному пределов этих функций.

То есть: если существует = А и существует , B ≠0, то существует .

(Доказать самостоятельно)

Теорема 5 (о пределе трех функций)

Если существуют равные конечные пределы функций f (x) и g (x) в точке :

= А

И при стремлении x к x₀ выполняется неравенство:

,

то существует .

Доказательство. Возьмем любое e > 0. Вычитая из всех частей двойного неравенства, данного в условии, число A, получим

(*)

Так как

,

то найдется такое d ₁, что для всех x ¹ x ₀, удовлетворяющих условию

,

будет верно неравенство

,

или, что, то же,

(*)

Аналогично для функции g (x) найдется такое d₂, что для всех x ¹ x ₀, удовлетворяющих условию

будет верно неравенство

(*)

Из неравенств, отмеченных (*) следует, что

,

или, что, то же самое

Для всех x ¹ x _0, удовлетворяющих условию 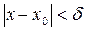, где d - меньшее из d ₁ и d ₂. Это означает, что

.

Теорема доказана.

6. Первый замечательный предел

Теорема 6. Предел функции в точке x = 0 существует и равен 1, то есть: .

Доказательство:

1) Пусть x > 0 (x )

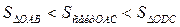(1)

; ;

(x – в радианах)

Подставим в соотношение (1) полученные значения площадей:

,

,

Так как все части двойного неравенства положительные, можно переписать так:

Т.к. то по теореме 5: .

2) Пусть x <0 (x )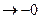

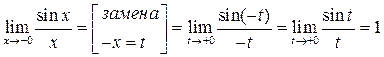(по доказанному в первом случае)

Следовательно, .

Теорема доказана.

Дата добавления: 2015-07-10