|
Читайте также: |
1. Рассмотрим в прямоугольных декартовых координатах непрерывно дифференцируемую функцию 
. Длина 
дуги кривой, заданной функцией , при изменении 
от 
до 
вычисляется по формуле:
. (15)
Подынтегральное выражение 
является дифференциалом длины дуги функции , т.е. 
.
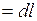2. Если кривая задана в параметрическом виде: 
, а 
[ 
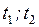], то длина дуги этой кривой вычисляется по формуле:
, (16)
где 
. Предполагается, что функции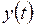 
и 
непрерывно дифференцируемы на промежутке [ ].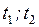
Дата добавления: 2015-07-11; просмотров: 80 | Нарушение авторских прав