Читайте также:
|
Вычисление площадей плоских фигур
1. Рассмотрим плоскую фигуру, ограниченную графиком функции 
и прямыми 
, 
, 
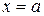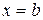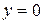, т.е. криволинейную трапецию (рис. 4).
|
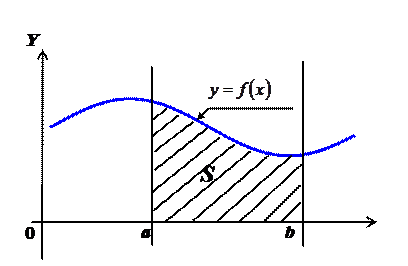
Рис. 4
Если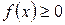 
, то площадь 
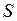такой фигуры вычисляется по формуле:
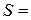
, (9)
где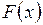 
− первообразная функции 
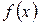, т.е. функция, у которой 
.
Если же функция 
на промежутке [ 
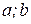] принимает как положительные, так и отрицательные значения, то площадь 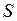вычисляется по формуле
.
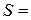
2. Если кривая 
задана в параметрическом виде: 
и 
, 
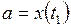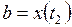, то
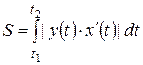. (10)
Предполагается, что функция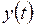 
непрерывна на промежутке [ 
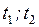], а функция 
непрерывно дифференцируема на промежутке [ ].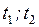
3. Теперь рассмотрим плоскую фигуру, которая ограничена снизу графиком функции 
, сверху − графиком функции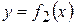 
, т.е.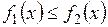 
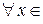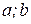[ ], а слева и справа − прямыми 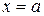, 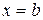(рис. 5).
Рис. 5
Площадь 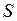такой фигуры находится по формуле
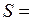
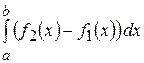. (11)
4. Если фигура, площадь которой нужно найти, ограничена прямыми 
и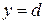 
, параллельными оси ОХ, прямой 
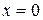и кривой 
, 
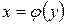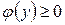, то эта фигура представляет собой криволинейную трапецию(рис. 6).
|
Рис. 6
Площадь такой фигуры вычисляется по формуле:
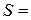
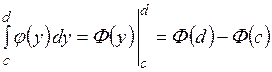, (12)
где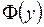 
− первообразная функции 
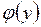, т.е. 
.
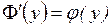5. Теперь рассмотрим плоскую фигуру, которая ограничена слева графиком функции 
, справа − графиком функции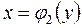 
, 
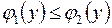, а снизу и сверху − прямыми и 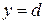(рис. 7).
Рис. 7
Площадь 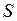такой фигуры находится по формуле
.
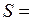
Дата добавления: 2015-07-11; просмотров: 236 | Нарушение авторских прав