Читайте также:
|
1. Объем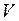 
тела, образованного вращением вокруг оси ОХ криволинейной трапеции, ограниченной графиком функции 
и прямыми 
, 
, 
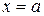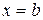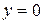(рис. 32), находится по формуле
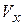
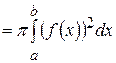. (19)
|
Рис. 32
2. Объем 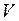тела, образованного вращением вокруг оси ОY криволинейной трапеции, ограниченной графиком функции 
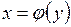и прямыми 
, 
, 
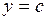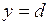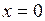(рис. 33), находится по формуле
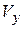
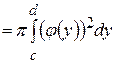. (20)
|
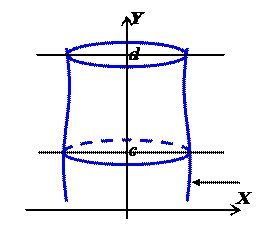
Рис. 33
3. Иногда объем 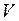тела, образованного вращением вокруг оси ОY криволинейной трапеции, ограниченной графиком неотрицательной функции и прямыми , (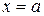
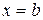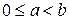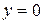), (рис. 34), удобно находить по формуле
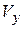
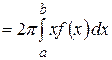. (21)
|
|
Рис. 34
Замечание. Если кривая, ограничивающая вращаемую криволинейную трапецию, задана в иной форме (в параметрическом виде или в полярных координатах), то в приведенных формулах нужно сделать соответствующую замену переменных.
Дата добавления: 2015-07-11; просмотров: 48 | Нарушение авторских прав
