Читайте также:
|
Площадь поверхности тела, образованного вращением вокруг оси ОХ криволинейной трапеции, ограниченной графиком функции 
и прямыми 
, 
, 
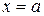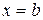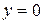(рис. 32), находится по формуле
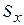
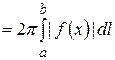, (22)
где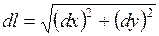 
− дифференциал дуги кривой . Если кривая задана в явном виде, то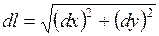 
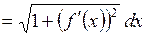и формула (22) примет вид: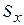 
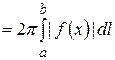
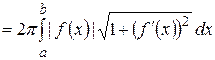. (23)
Если же кривая задана в параметрическом виде: 
и 
, 
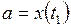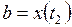, то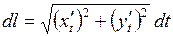 
. Предполагается, что функции 
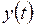и 
непрерывно дифференцируемы на промежутке [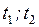 
]. В этом случае формула (22) примет вид:
.
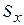
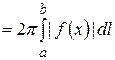
Дата добавления: 2015-07-11; просмотров: 51 | Нарушение авторских прав