Читайте также:
|
Подсчитаем среднее значение, которое касается СМО. Обозначим 
- число прибывающих заявок, 
- кот. обслужены (убывающие заявки). Разница между ними – это очередь. Рассмотрим график
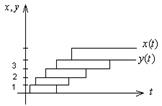
Представим, что ввели функцию 
. 
- промежуток времени, λ- плотность потока.
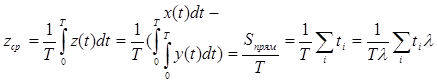
Графически этот интеграл равен сумме площадей прямоугольников.
- среднее количество заявок, которое прибывает за все время наблюдения
- среднее время пребывания заявки в системе 
- формула Литтла, кот. означает: среднее кол-во заявок в системе равно интенсивности потока, умноженного на среднее время пребывания заявки в системе.
Литтлу удалось док-ть, что эта формула справедлива:
1. при любом распределении потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания.
2. формула связывает среднее количество заявок в очереди с интенсивностью потока и среднем временем пребывания в очереди.
Таким образом, многие реальные СМО имеют точные решения или решения, полученные с помощью численных методов. И только наиболее сложные случаи требуют использования имитационного моделирования.
Дата добавления: 2015-07-11; просмотров: 213 | Нарушение авторских прав