Читайте также:
|
Погрешность – разница между точным значением величины и известным значением величины. Абсолютная погрешность – модуль этой разности. Известное значение называют приближённым. Погрешность возникает в случае неправильных исходных данных, в результате округления или упрощения математической задачи. Погрешность принято делить на три вида:
1) Неустранимая погрешность. Возникает из-за неточных исходных данных независимо от используемых методов и способов вычисления.
2) Погрешность метода – возникает из-за приближённого характера численных методов, которые используются при вычислениях (например,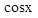 
и 
).
3) Вычислительная погрешность – это погрешность, связанная с ограниченным количеством разрядов ЭВМ.
Вычислительная ошибка всегда связанна с процедурой округления и само округление – попытка уменьшить вычислительную погрешность. Основная задача теории погрешности – оценить получаемую погрешность и предложить методы её уменьшения. Общая погрешность является суммой всех трёх видов погрешностей.
Опр 1. Абсолютной погрешностью приближенной величины 
называется модуль разности приближённого и точного значения величины: 
Опр 2. Относительной погрешностью 
называется отношение абсолютной погрешности к модулю приближённой величины: 
Абсолютную погрешность практически невозможно определить, т.к. не известно точное значение. Поэтому пользуются оценками величины.
По определению обе погрешности положительны, а относительная погрешность 
.
Дата добавления: 2015-07-11; просмотров: 107 | Нарушение авторских прав