Модели в экономике

Экономические науки – одна из наиболее важных сфер применения моделирования, именно здесь модели дают наибольшую эффективность, например если оптимизировать в одной модели траты всего государства, эффект будет выражаться в миллиардах долларов. Можно выделить следующие типы моделей:

l - модель ЛП (линейные) – модель ресурсов, запасов и т.д.

l - модели, построенные на транспортной задаче (распространение и перевозка грузов)

l - модели целочисленного программирования (результат принадлежит области целых чисел, количество человек, число заводов и т.д.) – модели первого типа с целочисленными параметрами.

l - модели динамического программирования – в основном связанные с развитием какого-либо производства, фирмы и т.д.

l - игровые модели, связанные с противоборством, конкуренцией.

l - прогностические модели, связанные с прогнозом ситуации при недостатке информации или случайных событиях.

l - модели автоматического управления (сделать систему управления оптимальной)

l нелинейные модели решаются только в отдельных случаях.

Стохастическое моделирование. Метод Монте-Карло в моделировании. Генерирование случайных и псевдослучайных чисел. Методы и алгоритмы генерации. Генерирование случайных чисел распределенных по экспоненциальному, нормальному и произвольно заданному закону распределения.

Стохастическое программирование – раздел математического программирования, совокупность методов решения оптимизационных задач вероятностного характера. Это означает, что либо параметры ограничений (условий) задачи, либо параметры целевой функции, либо и те и другие являются случайными величинами (содержат случайные компоненты).

Оптимизационная задача - экономико-математическая задача, цель которой состоит в нахождении наилучшего распределения наличных ресурсов. Решается с помощью оптимальной модели методами математического программирования, т. е. путем поиска максимума или минимума некоторых функций при заданных ограничениях (условная оптимизация) и без ограничений (безусловная оптимизация). Решение оптимизационной задачи называется оптимальным решением, оптимальным планом, оптимальной точкой.

Случайные величины характеризуются средними значениями, дисперсией, корреляцией, регрессией, функция распределения и т.д.

Статистическое моделирование – моделирование с использованием случайных процессов и явлений.

Существует 2 варианта использования статистического моделирования:

– в стохастических моделях может существовать случайные параметры или взаимодействия. Связь между параметрами носит случайный или очень сложный характер.

– даже для детерминированных моделей могут использоваться статистические методы. Практически всегда используются статическое моделирование в имитационных моделях

Модели, где между параметрами существует однозначная связь и нет случайных параметров называются детерминированными.

Детерминированные процессы – определенные процессы, в которых всякие процессы определены законами.

Человек считает все процессы детерминированными, однако со временем обнаружены случайные процессы. Случайный процесс – это такой процесс, течение которого может быть различным в зависимости от случая, причем вероятность того или иного течения определена.

Исследование процессов показало, что они бывают 2-х типов:

а) Случайные по своей природе процессы;

б) Очень сложные детерминированные процессы;

Доказана центральная теорема, в соответствии с которой сложение различных процессов увеличивает случайный характер. Так, если сложить совершенно разные последовательности, не связанные между собой, то результат в пределе стремится к нормальному распределению. Но известно, что нормальное распределение – независимые события, следовательно, объединение детерминированных событий в пределе ведет к их случайности.

Т.о. в природе не существует совершенно чисто детерминированных процессов, всегда есть смесь детерминированных и случайных процессов. Действие случайного фактора называется “шумом”. Источники шума – сложные детерминированные процессы (броуновское движение молекул).

В имитационном моделировании часто сложные процессы заменяют случайными, следовательно, для того чтобы сделать имитационную модель, нужно научиться моделировать случайные процессы методами статического моделирования. Представляют случайные процессы в КМ последовательностью случайных чисел, величина которых случайно меняется.

В статистическом моделировании очень часто используется метод статистических испытаний Монте-Карло. Метод Монте-Карло – это численный метод решения математических задач при помощи моделирования случайных величин.

Суть метода: для того, чтобы определить постоянную или детерминированную характеристику процесса можно использовать статический эксперимент, параметры которого в пределе связаны с определяемой величиной. Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину , математическое ожидание которой равно : . Практически же поступают так: производят испытаний, в результате которых получают 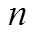возможных значений ; вычисляют их среднее арифметическое 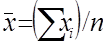и принимают 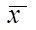в качестве оценки (приближенного значения) 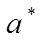искомого числа : .

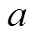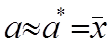Рассмотрим суть метода на примерах его использования:

Дата добавления: 2015-07-11