Модель колебательной системы

Рассмотрим ее от простого к сложному. В качестве примера могут служить очень многие окружающие на предметы, где важна вибрация (двигатели). Колебания свойственны и электрическим системам. Будем считать, что у нас одномерные колебания (вдоль одной оси).

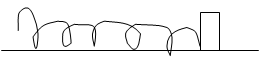
Положение предмета определяется одной координатой х, уравнение будет .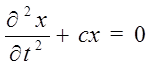

Решение этого диф. уравнения хорошо известно, оно представляет из себя

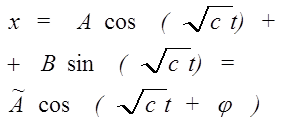
Колебания Гармонические со сдвигом фазы, незатухающие.

Усложняем модель - вводим затухание

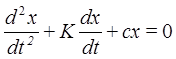(К- коэффициент затухания)

Если К мало (К<<1), то решение не будет сильно отличаться. Решение системы приводит к возникновению .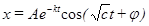

К=0,1- затухание хорошо видно (переодич.). При увеличении К (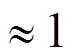)- апериодическое затухание, когда нет ни одного периода.

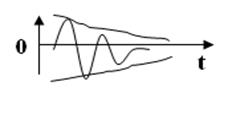
Дальше Усложняем задачу- введение периодичность внешней силы

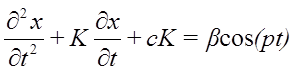
Собственная частота 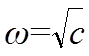, частота внутри силы р. Когда частоты равны, получаем резкое увеличение амплитуды колебаний - резонанс, 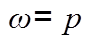. Если резонанс производить при колебании, собственные колебания затухнут, останутся вынужденные с частотой вынужденной силы.

К<<1, W>>p.

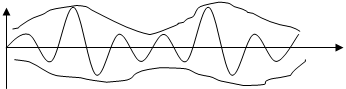
Модуляция. Внутри собственные колебания, их амплитуда моделируется с частотой собственных колебаний (биения)

Если К<0, м.б. 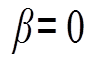(т.к. она только мешает) – параметрический резонанс.

Фактически параметрический резонанс при отрицательном затухании - это получение энергии извне. Процессы собственных колебаний важны, когда колебания паразитные (вредны), когда делают демпферы (делают затухания апериодичными).

Пример: рессоры автомобиля (обычно полезны для раскачки колебаний).

Резонанс может быть отрицательным и положительным по значению. Излучение электромагнитных волн основано на резонансах, как обычных, так и параметрических. Излучение и прием электромагнитных волн резонансные. Параметрический резонанс выгоден тем, что гораздо мощнее обычного. Это удобное средство для генерации, например, СВЧ-колебаний (магнитофон). Для параметрического резонанса собственная частота не нужна, поэтому можно вкачивать энергию до самого разрушения этого резонатора. Но может быть и вред, разрушение, что неприятно.

Модуляция – основа радиосвязи. Есть несущая частота, которую модулируют, а потом де модулируют. Звук низкочастотен (36 КГц), а радиоволна распространяется на высокой частоте, значит, нужны мегагерцы. Есть амплитудная, фазовая и частотная модуляция. Эффект биений обычно вредный, мешающий – это источник шума. Иногда с помощью биений делают специальные шумовые генераторы.

Модель теплопроводности тонкого слоя

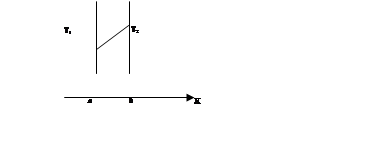
стекло (тонкое, длинное), 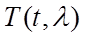- температура будет равномерна, следовательно 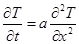. 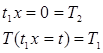гранич. 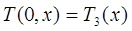Обычно это уравнение не решается в явном виде, а с помощью клеточной аппроксимации. Решая эту систему уравнений, мы находим значения в узлах сетки. Подобным же способом моделируются другие задачи теплопроводности, электростатики и электродинамики. Основная проблема – сложность вычисления, поэтому требуются мощные ЭВМ.

Еще одна модель – движение тела, брошенного под углом к горизонту. Для ее решения используют так называемый метод стрельбы, он уже близок к имитационному моделированию.

Еще – модель движения ракеты:

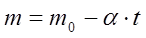
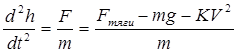- уравнение Циолковского.

Дата добавления: 2015-07-11