Читайте также:
|
В статическом моделировании принято источники случайных чисел называть генераторами. Обычно используют генератор случайных чисел равномерно распределенных на диапазоне от 0 до 1. Распределение называется равномерным, если вероятность появления числа на любом из отрезков одинакова. После создания генератора можно проверить, насколько равномерно его распределение. Это можно сделать методом Монте-Карло. Рассмотрим ПДСК (x;y) и построим окружность R=1. Вокруг окружности построим квадрат. Рассмотрим первую четверть:
Найдём площади квадрата и окружности:
Sкв.=1; Sчасти кр.= Sкр./4=πR2/4=π/4.
Проводим статистический эксперимент, для этого генерируем 2 последовательности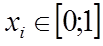 
и 
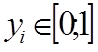. Пара этих чисел дает точку на плоскости 
. Т.о., эти две последовательности дают последовательность точек, но часть точек попадает в окружность, а часть будет вне окружности. Подсчитываем количество точек внутри Nвн. и общее количество точек Nобщ.. С точки зрения теории вероятности, если множество точек равномерно распределено по площади, то кол-во точек зависит от размера площади:
.
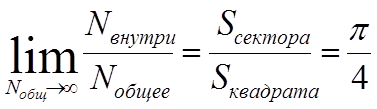Проверяем, так ли это в нашем эксперименте. В принципе точно π/4 мы не получим, но должны получить число близкое к нему. Проводят несколько экспериментов, а потом найденную величину усредняют.
Если средняя величина ближе к π/4, чем каждое из вычисленных величин, то считают, что гипотеза о равномерном распределении оказалась правильной. Для метода Монте-Карло это характерно: делаем гипотезу, затем проводим статистический эксперимент и проверяем эту гипотезу. Если гипотеза справедлива, то распределение равномерно, в противном случае – не равномерно.
Дата добавления: 2015-07-11; просмотров: 97 | Нарушение авторских прав