
|
Читайте также: |
О1. Корень 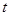 отделен на отрезке
отделен на отрезке 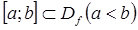 , если
, если 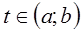 и других корней в этом отрезке нет. При этом
и других корней в этом отрезке нет. При этом 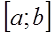 называется отрезком изоляции корня
называется отрезком изоляции корня 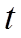 .
.
Отделить корни уравнения - значит для каждого из корней найти свои отрезки изоляции.
О2. Поиск приближенного значения корня с точностью до заданного достаточно малого числа 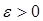 называется уточнением этого корня.
называется уточнением этого корня.
Следовательно, задача уточнения будет решена, если найдется число 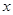 такое, что
такое, что  . Тогда
. Тогда  с точностью до
с точностью до 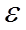 .
.
Если отрезок 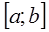 изоляции корня
изоляции корня 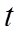 найден, то любое число из него можно взять в качестве приближенного корня. Например,
найден, то любое число из него можно взять в качестве приближенного корня. Например,  . Пусть
. Пусть 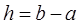 – длина отрезка. Поскольку
– длина отрезка. Поскольку 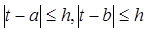 , концы отрезка являются приближениями к
, концы отрезка являются приближениями к 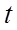 с точностью до
с точностью до 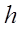 . Легко проверить, что
. Легко проверить, что 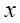 имеет точность до
имеет точность до 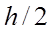 , т.е. обладает лучшей характеристикой точности.
, т.е. обладает лучшей характеристикой точности.
Чем меньше длина отрезка изоляции, тем выше точность приближения, однако с помощью используемых для отделения корней приемов получить отрезок достаточно малой длины трудно. Нужны специальные методы уточнения корней. Далее будет рассмотрено несколько таких методов, которые реализуют следующие два способа поиска приближенного корня с заданной точностью 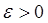 :
:
1. Последовательно уменьшая длины отрезка изоляции корня по какому-либо правилу, отыскивается отрезок 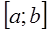 такой, что
такой, что 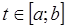 и
и  . Тогда приближенным корнем требуемой точности будет середина отрезка
. Тогда приближенным корнем требуемой точности будет середина отрезка 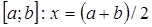 .
.
2. Строится последовательность чисел 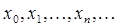 , сходящаяся к корню
, сходящаяся к корню 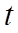 . Как только окажется
. Как только окажется 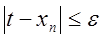 , можно положить
, можно положить 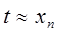 . Такая последовательность называется последовательностью приближений, а определяющий её метод – методом последовательных приближений.
. Такая последовательность называется последовательностью приближений, а определяющий её метод – методом последовательных приближений.
Первый способ удобен тем, что позволяет легко устанавливать завершение процесса уточнения, поскольку отрезки изоляции и их длины на каждом шаге вычислений известны.
Непосредственную проверку условия 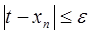 из второго способа проводить не удается, ибо известен только корень
из второго способа проводить не удается, ибо известен только корень 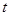 . В то же время для каждого метода последовательных приближений есть возможность получить неравенства вида
. В то же время для каждого метода последовательных приближений есть возможность получить неравенства вида
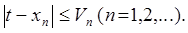 (2)
(2)
Здесь 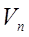 – числовое выражение, значения которого при каждом
– числовое выражение, значения которого при каждом 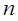 характеризуют степень близости приближения
характеризуют степень близости приближения 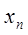 к корню, обеспечиваемую данным методом. Из (2) следует, что за условие окончания процесса приближений можно взять неравенство:
к корню, обеспечиваемую данным методом. Из (2) следует, что за условие окончания процесса приближений можно взять неравенство:  .
.
Неравенство (2) позволяет решить и задачу определения абсолютной погрешности каждого приближения  , ибо ясно, что
, ибо ясно, что  .
.
Таким образом, отделить корни, значит задать такие отрезки, на которых корень существует и он единственный. Полученный отрезок будет интервалом неопределенности корня, а половина длины отрезка – оценкой абсолютной погрешности. Отделение корней обычно производится графически и (или) аналитически.
Графический способ отделения корней уравнения (1) заключается в поиске таких отрезков 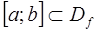 , внутри которых находится абсцисса точки пересечения графика функции
, внутри которых находится абсцисса точки пересечения графика функции 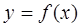 с осью
с осью 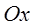 , т.е. нуль функции
, т.е. нуль функции  .
.
Дата добавления: 2015-07-11; просмотров: 173 | Нарушение авторских прав