Б) Приближенный аналитический метод (проверка изменения знака).

Основа метода – теорема мат.анализа:

Т1:(первая т. Больцано-Коши) Пусть функция определена и непрерывна на отрезке 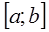, причем на концах его принимает значения разных знаков, т.е. . Тогда существует по крайней мере одна точка , в которой значение функции равно нулю.

Т.е. если функция меняет знак на отрезке, то на этом отрезке она меняет корень.

Мы можем разбить весь отрезок на n частей, и проверить на каких частях функция меняет знак. Эти отрезки можно считать отрезками отделённых корней.

Приведем примерный алгоритм отделения корней уравнения аналитически:

1. Задается отрезок [а,b], на котором необходимо отделить корни функции f(х).

2. Задается начальное значение n и строится сетка х_i =а+ih, h=(b-a)/n, i =0,1,2,...,n. Сетка делит отрезок на n частей с помощью n+1 точки.

3. Вычисляется значение функции f(х_i)=f_i, и вычисляется произведение значе­ний функции на концах отрезка f_i*f_i+1, i =0,1,2,...,n+1.

4. Подсчитываем количество отрицательных произведений и запоминаем от­резки, где произведение отрицательно или равно 0. Число таких отрезков k. Каждый из таких отрезков должен содержать хотя бы 1 корень.

5. Увеличиваем n в два раза и повторяем процедуру. Получаем новое количе­ство отрезков (корней) k_i.

Если {k<k₁ è k=k₁ и повторяем п.5 {k=k₁ è выход

Дата добавления: 2015-07-11