
Читайте также:
|
Поиск – задача определения максимума или минимума функции, она сложная для многомерного случая. Если нет дополнительных условий-ограничений, то можно использовать методы градиентного поиска и метод координатной релаксации. Но существует возможность использовать и метод Монте-Карло:
Пусть задана некая область 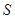 в системе координат. В этой области есть одна точка экстремума (максимума или минимума). Нужно найти эту точку. Для метода Монте-Карло сгенерируем две последовательнсти: n, сгенерируем
в системе координат. В этой области есть одна точка экстремума (максимума или минимума). Нужно найти эту точку. Для метода Монте-Карло сгенерируем две последовательнсти: n, сгенерируем

 ,
,  ,
,  и
и 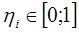 , где
, где  ,
,  ,
, 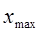 ,
, 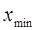 - границы области
- границы области 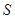 . Тогда
. Тогда 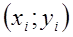 точки лежат в области. Вычислим в этих точках значения функций
точки лежат в области. Вычислим в этих точках значения функций  . Затем среди этих значений найдем максимальное/минимальное. По теории вероятности следует, что если количество опытов устремить в бесконечность, то это экстремальное значение стремится к искомому значению. Тогда существуют следующие варианты:
. Затем среди этих значений найдем максимальное/минимальное. По теории вероятности следует, что если количество опытов устремить в бесконечность, то это экстремальное значение стремится к искомому значению. Тогда существуют следующие варианты:
а) простой поиск, берем побольше точек и считаем, что максимальное значение соответствует нашему максимальному значению;
б) поиск с аккомодацией – проводим несколько экспериментов, но каждый раз область уменьшаем так, чтобы максимальное значение было в центре. При этом центр области выбирается в текущем максимальном значении. Очевидно, что этот метод более быстрый и требует меньше случайных точек, так как при этом уменьшается область, их плотность увеличивается.
в) метод последовательного поиска – точки с самого начала берутся в маленьком окошке, но это окошко перемещается так от шага к шагу, чтобы максимальное значение было в центре.
Так как во 2 и 3 случаях повторять процесс можно до бесконечности, то мы остановимся тогда, когда размер области или расстояние перемещения для центра окна меньше заданной погрешности. Существуют так же варианты, которые совмещают в себе 2-й и 3-й подходы.
В статистич. моделировании принято использовать случайные числа, кот-е наз генераторами. Обычно используют генератор случ чисел равномерно распределенных на диапазоне от 0 до 1. Имея такой генератор можно строить все другие последовательности. Распределение наз равномерным если вероятность появления на любом из отрезков равновероятна. Вероятность на отрезке прямопропорциональна длине отрезка.
Псевдослучайные числа отличаются от случайных тем, что они не случайные, но очень похожи на случайные, фактически они генерируются по формуле:.
xi+ 1= f (xi, xi -1,…)
Псевдослучайная последовательность всё время одна и та же, повторяется, её менять можно только меняя точку входа.Как правило, в псевдослучайной последовательности существует период Т, т.е. через период элемент повторяется: xi+ Т= xi. Этот период должен быть больше чем длина последовательности. Последействие выражается в том, что есть корреляция между элементами. Корреляция – это зависимость между двумя последовательностями случайных чисел, определяется коэффициентом корреляции.Для построения генератора равномерно распределенной пос-ти дейст-х чисел от 0 до 1 исполь. следующие методы:
1) аппаратный, в этом мет-е генер-р предст-т из себя отдельный прибор, в кот-м есть источник шума, теплового, квантового или радиоактив-го. Тепловой шум может создавать радиоакт. лампа или полупроводниковый прибор. Однако данный вариант не очень надежен, т.к. накладные шумы от внешней температуры. Источник квантового шума-это туннельный диод. Это самый дешевый способ, есть проблема надежности из-за влияния окружающей среды. Радиоакти-й источник надежно, но дорого. Аппарат создает эл. эмпульсы величина или расстояние м/д кот-ми меняется случ. образом. Далее спец. схема оцифровки превращает этот сигнал в после-ть чисел.
2) табличный, кем-то спец-м образом сгенерированы десятки-тысяч чисел, к-рые проверены и помещены в спец. таблицу, таб. расположена в файле, оттуда мы можем брать начиная с любого места нужную нам пос-ть чисел. Здесь одна проблема таб. должна быть большой.
3) алгоритмический, исполь-ся итерац-я фор-ла вида  по кот-ой выч-ся эл-ты пос-ти псевдослучайных чисел. Псевдослуч-ое число похоже на слу-ое, но опреде-ся всетаки детерминированным процессом т.е. итерац. фор-ой. Изуч-е псевдослуч. чисел показывает, что по сравнению с случ числами у них есть след. недостатки: а)каждый раз генерир-ся одна и таже пос-ть;б) в этой пос-ти есть период Т, такой, что
по кот-ой выч-ся эл-ты пос-ти псевдослучайных чисел. Псевдослуч-ое число похоже на слу-ое, но опреде-ся всетаки детерминированным процессом т.е. итерац. фор-ой. Изуч-е псевдослуч. чисел показывает, что по сравнению с случ числами у них есть след. недостатки: а)каждый раз генерир-ся одна и таже пос-ть;б) в этой пос-ти есть период Т, такой, что  ; в)в пос-ти есть последействия, т.е. текущий эл-т зависит от предшествующих, хотя для настоящих случ. чисел такой пос-ти не должно быть. Последействие опред-ся спец фун-ей корреляцией, к-ая опред-т зависим-ть м/д величинами. В тоже время алгоритмический генер. обладает большими достоинствами- нет необ-ти покупать спец. прибор, можно всегда сгенирировать столько чисел сколько нужно не занимая места на диске, поэтому ученые стали стали изучать различные генер-ы пытаясь сделать так, чтобы период был очень большим, последействие очень мало, а первая проблема снималась тем, что точка входа в итерац-ю посл-ть постоянно меняется, т.е.меняется
; в)в пос-ти есть последействия, т.е. текущий эл-т зависит от предшествующих, хотя для настоящих случ. чисел такой пос-ти не должно быть. Последействие опред-ся спец фун-ей корреляцией, к-ая опред-т зависим-ть м/д величинами. В тоже время алгоритмический генер. обладает большими достоинствами- нет необ-ти покупать спец. прибор, можно всегда сгенирировать столько чисел сколько нужно не занимая места на диске, поэтому ученые стали стали изучать различные генер-ы пытаясь сделать так, чтобы период был очень большим, последействие очень мало, а первая проблема снималась тем, что точка входа в итерац-ю посл-ть постоянно меняется, т.е.меняется  .
.
Генератор Фон-Неймана. Исторически одним из1-ых был предложен Ф- Ней., но использовал метод середины квадрата. Пусть  начальное целое число, ко-ое состоит из 5 цифр. Тогда квадрат этого числа будет содержать 10 цифр, тогда возьмем из середины этого числа 5 цифр. Эти 5 цифр дадут число
начальное целое число, ко-ое состоит из 5 цифр. Тогда квадрат этого числа будет содержать 10 цифр, тогда возьмем из середины этого числа 5 цифр. Эти 5 цифр дадут число  . В рез-те такого проц-са получ послед-ть чисел, кот-ые похожи на случ-ые
. В рез-те такого проц-са получ послед-ть чисел, кот-ые похожи на случ-ые  их можно представить как дробную часть числа распределенную от0 до 1. Однако изуч. этой посл-ти показало, что в ней возник-т проц-ы вырождения. Обычно число приходит к 0 или 1. Поэтому этот мет-д не получил большого распространения.
их можно представить как дробную часть числа распределенную от0 до 1. Однако изуч. этой посл-ти показало, что в ней возник-т проц-ы вырождения. Обычно число приходит к 0 или 1. Поэтому этот мет-д не получил большого распространения.
Линейный конгруэнтный метод. Он сущ. в 2-х вариантах виде смешанного генератора (Леммера) 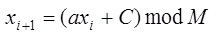 и мультипликативного
и мультипликативного  . Мультипликативный–частный случай смешанного при с=0. Было док-но, что период такого генератора яв-ся простым сомножителем числа М
. Мультипликативный–частный случай смешанного при с=0. Было док-но, что период такого генератора яв-ся простым сомножителем числа М  что М выгоднее выбирать простым числом, чтобы период был больше. Возникла проблема найти такие большие простые числа. Очень удачным оказалось число Мерсона-это наибольшее простое число, к-ое могло быть записано в 32-х разрядах ЭВМ, т.к. долгое время компью-ы были 32-х разрядными. То число Мерсона стало стандартным
что М выгоднее выбирать простым числом, чтобы период был больше. Возникла проблема найти такие большие простые числа. Очень удачным оказалось число Мерсона-это наибольшее простое число, к-ое могло быть записано в 32-х разрядах ЭВМ, т.к. долгое время компью-ы были 32-х разрядными. То число Мерсона стало стандартным  . Кроме числа Мерсона матем-ки исследовали посл-ть при различных значениях а и с, были найдены оптимальные значения а и с.
. Кроме числа Мерсона матем-ки исследовали посл-ть при различных значениях а и с, были найдены оптимальные значения а и с.
Сдвиговый генератор Таусворта. Выпол. выч-я в таб. приходится не с 10-ми числами, а с двоичными. Поэтому Таусворд предложил модификацию генератора Леммера с учетом двоичных вычислений. На каждом шаге приходится умножать и делить целые числа, что довольно сложно в двоичной системе. Поэтому он предложил заменить эти операции на двоичное умножение и взятие двоичного остатка. Вместо больших чисел в его итерац-х числах получили разряды двоичных чисел 0 или 1. Если брать вместо числа М число 2, то фактическое значение последнего разряда произведения, определяется умножением последних разрядов произведения. Т.о. в методе Таусворда мы фактически вычисляем только 1 разряд по предыдущему разряду. 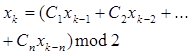 в рез-те действия генератора Таусворда формируется длинная пос-ть 1 и 0. Наилучший период
в рез-те действия генератора Таусворда формируется длинная пос-ть 1 и 0. Наилучший период  , n –число разрядов числа С. Далее из этой пос-ти 1 и 0 можно нарезать разных чисел. Данные генераторы были использованы с помощью следующих тестов: 1) тест на равномерность распределения; 2) тест на последействие, использовалась корреляция; 3) выборочный тест; 4) определение периода. Для того, чтобы улучшить качества генератора были созданы спец. методы улучшения кач-ва: метод возмущений и модификация с использованием разных последовательностей.
, n –число разрядов числа С. Далее из этой пос-ти 1 и 0 можно нарезать разных чисел. Данные генераторы были использованы с помощью следующих тестов: 1) тест на равномерность распределения; 2) тест на последействие, использовалась корреляция; 3) выборочный тест; 4) определение периода. Для того, чтобы улучшить качества генератора были созданы спец. методы улучшения кач-ва: метод возмущений и модификация с использованием разных последовательностей.
Экспоненциальное. 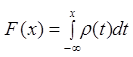 . Пусть у нас есть случ. величина
. Пусть у нас есть случ. величина  - равномерно распределена.
- равномерно распределена. 
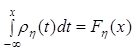




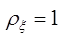

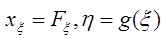 . Мы должны
. Мы должны  , чтобы найти
, чтобы найти 
 . Т.о.чтобы получить
. Т.о.чтобы получить 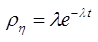 мы должны все значения
мы должны все значения  преобразовать в
преобразовать в 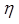 . Т.о. можно получить любое распределение. Если мы можем найти в явном виде его фун-ю распределения. В данном примере мы получили фор-лу с помощью которой можно получить по равномерному распределению экспоненциальное расп-е, т.е. если
. Т.о. можно получить любое распределение. Если мы можем найти в явном виде его фун-ю распределения. В данном примере мы получили фор-лу с помощью которой можно получить по равномерному распределению экспоненциальное расп-е, т.е. если  распределено равномерно на [0;1], то
распределено равномерно на [0;1], то  будут распределяться по экспо-у закону
будут распределяться по экспо-у закону 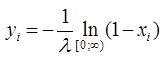 .
.
Нормальное.  ,
,  . Взять первообразную от этой фун-и нельзя, но можно воспользо-ся методом сложения посл-ти. Пусть мы с помощью генератора генерируем не 1 пос-ть, а несколько
. Взять первообразную от этой фун-и нельзя, но можно воспользо-ся методом сложения посл-ти. Пусть мы с помощью генератора генерируем не 1 пос-ть, а несколько  строим сумму.
строим сумму.  , где N-число посл-тей. В соответствии с центр. Теоремой теоремой вероятности, чем больше будет таких пос-тей, тем ближе распред-е
, где N-число посл-тей. В соответствии с центр. Теоремой теоремой вероятности, чем больше будет таких пос-тей, тем ближе распред-е  будет ближе к нормальному. Для получения нормального распределения нужно 5 раз сгенерировать равномерно распределенные пос-ти. Затем сложить м/д собой эти пос-ти и найти их среднее.
будет ближе к нормальному. Для получения нормального распределения нужно 5 раз сгенерировать равномерно распределенные пос-ти. Затем сложить м/д собой эти пос-ти и найти их среднее.
Произвольное. Метод дистограмм наиболее трудоемкий, но зато позволяет построить любое расп-е, кот-ое задано графиком плотности. Разделим отрезок [a; b] на n равных частей длиной  . В концах отрезка восстановим значение фун-и, это будут узлы.
. В концах отрезка восстановим значение фун-и, это будут узлы.  ,
,  -высота столбика.
-высота столбика.  -относительная высота.
-относительная высота. 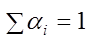 Высота прямоугольников
Высота прямоугольников  д.б. пропорциональна отрезку
д.б. пропорциональна отрезку 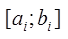 .
.  -вероятность, что
-вероятность, что  отсюда и идея метода дистограмм. Если мы будем распределять случ.числа по этим отрезкам так, чтобы внутри отрезка вер-ть была равномерна, а м/д отрезками опред-сь бы вероя-тью
отсюда и идея метода дистограмм. Если мы будем распределять случ.числа по этим отрезкам так, чтобы внутри отрезка вер-ть была равномерна, а м/д отрезками опред-сь бы вероя-тью  . Чем больше будет этих отрезков, тем больше фун-я будет похожа на заданную, т.е. лучше будет аппроксимация.На каждом отрезке распределение равномерное
. Чем больше будет этих отрезков, тем больше фун-я будет похожа на заданную, т.е. лучше будет аппроксимация.На каждом отрезке распределение равномерное 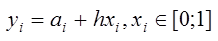 нужно эти отрезки переводить по очереди. Отсюда 1-ый вариант послед-но прямоуг-к за прямоуг-ом генерирует эти числа. Возникает проблема, что вер-ть попадания в каждый прямоуг-к разная зависит от высоты
нужно эти отрезки переводить по очереди. Отсюда 1-ый вариант послед-но прямоуг-к за прямоуг-ом генерирует эти числа. Возникает проблема, что вер-ть попадания в каждый прямоуг-к разная зависит от высоты  кол-во точек которое попадает в каждый прямоуг-к разное и пропорциональное
кол-во точек которое попадает в каждый прямоуг-к разное и пропорциональное 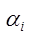 . Мы могли бы опред-ть кол-во точек для каждого отрезка, если бы знали общее кол-во точек, которое нам потребо-сь, но это известно не всегда. Поэтому предлаг-ся другой способ распределение чисел равномерно. Возьмем отрезок [0;1] разобьем на n частей, но не равных а пропорциональных
. Мы могли бы опред-ть кол-во точек для каждого отрезка, если бы знали общее кол-во точек, которое нам потребо-сь, но это известно не всегда. Поэтому предлаг-ся другой способ распределение чисел равномерно. Возьмем отрезок [0;1] разобьем на n частей, но не равных а пропорциональных  .
.  Тогда на [0;1] будут отрезки
Тогда на [0;1] будут отрезки 
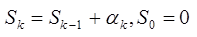
 пусть мы генерируем случ числа
пусть мы генерируем случ числа 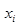 равномерно распределенные. Тогда вер-ть того, что
равномерно распределенные. Тогда вер-ть того, что  попаджет на к отрезок будет равна длине этого отрезка
попаджет на к отрезок будет равна длине этого отрезка  . Мы получили следующие
. Мы получили следующие  преобразования по формуле
преобразования по формуле  тогда
тогда 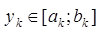 причем вероя-ть попадания в этот отрезок равна
причем вероя-ть попадания в этот отрезок равна  . Значит, что мы построили распределение для
. Значит, что мы построили распределение для  виде дистограмм.
виде дистограмм.
Моделирование потоков случайных событий. Сис-мы массового обслуживания. Основные понятия и хар-ки потоков. Класс-ция с-м масс.обс-ния. Оценка осн. Парпметров сис-м обс-ния(очередь, время ожидания)Формула Литтла.
Поток событий - последова-ть случ. событий, следующих одно за друг, в какие-то случ. моменты времени. Напр. поток вызовов на телефонной станции, поток ж.д.составов, поступающих на сортировочную станцию. Поток событ. можно наглядно изобразить рядом точек на оси времени Ot, положение кажд. из них случайно. Событ., образующие поток, сами по себе вероят-ми не обладают; вер-тями облад. др., производные от них события. В реальности события и заявки могут быть 2 видов:
1) однородные –это те заявки, которые всегда одинаковые по виду обслуживания.
2) неоднородные – обслуживаются по разному. При этом заявки в потоке считаются неодновременными и практически мгновенными. Поток, в кот. не могут быть двух заявок одновременно, назыв. одинарным. Между событиями есть промежутки времени. Если эти промежутки времени строго фиксированы, то такой поток называется регулярным. Если время между событиями меняется случайно, то такой поток называется случайным. Доказано, что любой неоднородный поток может стать однородным, если его время обслуживания соединять с промежутками между событиями. Стационарный поток – это случайный поток, характеристика которого не меняется со временем. Под характеристикой понимается плотность потока λ, которая равна среднему количеству заявок, проходящих за ед. времени. Одинарный поток назыв. ещё простейшим потоком. Интенсивность потока (  )-сред. число событий, приходящееся на ед. времени. Интенс-ть может быть постоянной и зависящей от времени t.
)-сред. число событий, приходящееся на ед. времени. Интенс-ть может быть постоянной и зависящей от времени t.
Регулярный поток -когда соб. следуют одно за другим ч/з определенные равные промежутки времени.
Ещё одна характеристика: распределение определяет вероятность того, что событие произойдёт в какой-то промежуток времени.
Пуассоновский поток – это поток без последействия, т.е. вероятность появления события не зависит от предшествующих событий. Этот поток является наиболее случайным из всех возможных. Стационарный пуассоновский поток имеет следующее распределение (которое называется распределением пуасона):Pm(τ)=(λτ)m/m!*e-λτ, где λ – плотность потока; τ – промежуток времени;m – кол-во событий
Если пуассон-ий поток не стационарен,то P0(τ,t0)=am/m!*e-a.
Функция λ(t) – это функция, которая показывает зав-сть плотности потока от времени для нестационарного режима.В любой фиксированный момент λ(tф)= λф – мгновенная плотность. Совершенно случайным потоком явл. только пуассоновский. Потоки с другим распределением можно представить как сумму случ. и детерминированных потоков. Причём случайная составляющая может представляться как сумма нескольких пуассоновских потоков с различным λ. → пуассоновские потоки должны иметь последействие, т.е. вероятность появления нового события от предшествующих событий.
Поток Пальма – это пуассоновский поток, в кот. на последействие наложены ограничения.Обычно потоки Пальма образуются с пом. потоков Эрланга (они наз. ещё рекуррентными).Потоки Эрланга можно получить из пуассоновских потоков путём просеивания. Если из потока выбирать каждую вторую заявку, то это поток Эрланга второго порядка, каждую третью – третьего и т.д.Док-но, что чем > порядок потока Эрланга, тем > последействие. При n→∞ получим регулярный поток. Тогда пуассоновский поток это поток Эрланга 1-го порядка. Следует учитывать, что для создания потоков Эрланга исп-ся стационарные потоки. Поэтому стационарный пуассоновский поток называют простейшим.
СМО – это дискретные системы, которые могут быть как стахостические, так и детерминированные. Обычно это стахостические. Обычно СМО решается как имитационная модель. Началом теории СМО было решение задачи Эрланга: в 20-е годы ХХв. в Европе проходил процесс телефонизации. Эрланга телефонная компания попросила решить их проблему.Дано n-абонентов. Все они связаны с телефонной станцией. Проблема возникает, когда абоненты связываются с абонентами другой ТС. Между станциями существует m каналов, каждый канал – это дорогая вещь. Поэтому каналов < абонентов, т.е. m<n и возможна ситуация когда все каналы заняты, тогда абонент получает отказ (сбой) соединения. Фирма попросила определить оптимальное число каналов, чтобы с одной стороны их было поменьше (т.е. стоимость <), а качество соединения удовлетворяло заданным требованиям.
 Т.е. может задаваться кол-во отказов до соединения, либо среднее время ожидания соединения. Эрланг провёл исследование реальной ТС, нашёл вероятности обслуживания абонентов, построил кривую потока заявок в соответствии с кот. была изменена тарифная система. Он определил основные характеристики такой системы обслуживания – это средняя пропускная возможность канала, среднее время обслуживания и среднее количество отказов. Он получил систему ДУ для вероятности нахождения системы в каком-то состоянии. Аналогичную систему разработал Марков при изучении Марковских процессов. В дальнейшем оказалось, что системы типа СМО чрезвычайно распространены:А) торговля Б) транспорт В) многие технологические процессы и особенно работа персонала, т.к. человек всегда поступает довольно хаотично Г) элементы систем массового обслуживания были найдены в различных экономических системах Д) системы связи и коммуникации, компьютерные сети и сама ЭВМ.
Т.е. может задаваться кол-во отказов до соединения, либо среднее время ожидания соединения. Эрланг провёл исследование реальной ТС, нашёл вероятности обслуживания абонентов, построил кривую потока заявок в соответствии с кот. была изменена тарифная система. Он определил основные характеристики такой системы обслуживания – это средняя пропускная возможность канала, среднее время обслуживания и среднее количество отказов. Он получил систему ДУ для вероятности нахождения системы в каком-то состоянии. Аналогичную систему разработал Марков при изучении Марковских процессов. В дальнейшем оказалось, что системы типа СМО чрезвычайно распространены:А) торговля Б) транспорт В) многие технологические процессы и особенно работа персонала, т.к. человек всегда поступает довольно хаотично Г) элементы систем массового обслуживания были найдены в различных экономических системах Д) системы связи и коммуникации, компьютерные сети и сама ЭВМ.
СМО принято классифицировать двумя способами:
1. по типу потоков событий-заявок; 2. по дисциплине обслуживания.
Т.е. в общем случае СМО представляет из себя устройство для обслуживания, на которое поступает поток заявок. Устройство может обслужить заявку или сделать отказ.
Примеры СМО:
1. Ремонтная зона в автохозяйстве и автобусы, сошедшие с линии из-за поломки.
2. Травмопункт и больные, пришедшие на прием по случаю травмы
3. Телефонная станция с одним входом и абоненты, которых при занятом входе ставят в очередь.
СМО обозначают с помощью графосостояний:
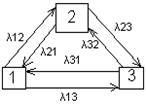 где 1,2,3 – это вершины, состояния; ребра – это переходы из одного состояния в другое;
где 1,2,3 – это вершины, состояния; ребра – это переходы из одного состояния в другое;  - плотность потока; p - вероятности события. Можно для каждого состояния задать вер-ть того, что система нах-ся в каком-то состоянии. В теории массового обслуживания часто встречается схема гибели и размножения, если граф состояний системы представ. собой «схему гибели и размножения», то уравнение Колмогорова, алгебраич. ур-ия для финальных вероятностей для некоторых случаев удается решить заранее, в буквенном виде.
- плотность потока; p - вероятности события. Можно для каждого состояния задать вер-ть того, что система нах-ся в каком-то состоянии. В теории массового обслуживания часто встречается схема гибели и размножения, если граф состояний системы представ. собой «схему гибели и размножения», то уравнение Колмогорова, алгебраич. ур-ия для финальных вероятностей для некоторых случаев удается решить заранее, в буквенном виде.
Уравнения Колмогорова-Эрланга:
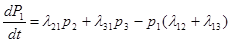
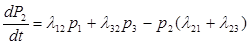
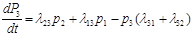 , где
, где  .
.
Причем входящий поток идет с «+», исходящий – с «–».
Ур-я хар-ны для колебательной системы, в них есть переходные процессы, а затем система переходит к устойчивому, равновесному состоянию. марков и Колмогоров док-ли, что через опред-ое время устанавливается равновесное – финитное – состояние. Чтобы получить финитное состояние, необх-мо, чтобы все вер-ти =0:
 . Тогда финитное решение ур-я Колмогорова-Эрланга:
. Тогда финитное решение ур-я Колмогорова-Эрланга:



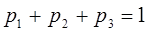
Решая эти уравнения можно определить характеристики СМО:
1)средняя загруженность узлов обслуживания; 2)среднее время обслуживания заявки; 3)среднее время ожидания в очереди; 4)средняя длина очереди.
В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует.В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности быть обслуженной. Эти СМО чаще встречаются на практике. Обслуживание с приоритетом - когда заявки обслуж-ся вне очереди. Абсолютный приоритет – когда заявка с более высоким приоритетом «вытесняет» из-под обслуживания заявку с низшим. Относительный приор. - когда начатое обслуживание доводится до конца, а заявка в более высоким приоритетом имеет лишь право на лучшее местов очереди. СМО с многофазовым обслуживанием – состоит из нескольких последовательных этапов или фаз. В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО (ск-ко каналов занято). В замкнутой СМО – зависят.
Рассмотрим схему гибели-размножения (автор Эрланг). Здесь возможны только переходы между соседними состояниями. Граф представляет собой ленту:
 Составим уравнения:
Составим уравнения:  (1)
(1)
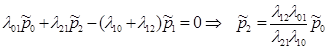 Т.о.,
Т.о., 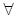 последующее значение можно выразить через
последующее значение можно выразить через 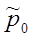 .
.
 ,
,  ,
,  ,
, 
Так как  , Эта формула позволяет рассчитать вероятность
, Эта формула позволяет рассчитать вероятность  , не решая системы уравнений, то
, не решая системы уравнений, то 
 .
.
Дата добавления: 2015-07-11; просмотров: 198 | Нарушение авторских прав