Интерполяция и аппроксимация функций

Аппроксимация – замена одной функции на другую, удовлетворяющую условию близости. Условие близости – строгое математическое ограничение, которое позволяет в идеале выбрать единственную функцию. Функция, которую заменяют при аппроксимации принято называть аппроксимируемой. Функцию, которой заменяют аппроксимируемую принято называть аппроксимирующей. Смысл аппроксимации в том, чтобы более сложную или неявную аппроксимируемую функцию заменить более простой аппроксимирующей. Поэтому аппроксимирующие функции, как правило, элементарные – полиномы, тригонометрические функции и т.д.

Интерполяция – вид аппроксимации, для которого условие близости – совпадение значений функций в отдельных точках (узлах интерполяции). Пусть задан отрезок [a,b] на котором строится интерполирующая функция L(x) для интерполируемой F(x). Этот отрезок разбиваем на n частей точками x_i = a+i*h –узлами интерполяции, где h = (b-a)/n. Это вариант равноотстоящих узлов. В общем случае узлы расположены произвольно, но при этом одна из точек совпадает с a, а другая с b. Пронумеруем точки так, чтобы они распределились по возрастанию: а= х₀ < х₁ < х₂ < … < х_n = b. При этом необходимо, чтобы точки не совпадали между собой. В узлах интерполяции зададим значения интерполируемой функции y_i = F(x_i). Значения индекса меняются i=0,1,2,…n-1. Таким образом, задаются 2 набора значений x_i, y_i, которые должны быть связаны условием интерполяции (условием близости) L(x_i) = y_i. Практически это совпадение функций L(x) и F(x) в узлах интерполяции. Этот вариант осуществляется, например, при построении графика функции по точкам. Принято приближение функции F(x) интерполирующей L(x) на отрезке [a,b] называть собственно интерполяцией, а вне данного отрезка экстраполяцией. Погрешностью интерполяции называют величину d(x)=|L(x) - F(x)|.

На графике видно, что в узлах интерполяции погрешность равна нулю. Между узлами интерполяции погрешность положительна и не равна нулю, а в областях экстраполяции быстро растет.

Существуют различные варианты интерполяции (полиномиальная, тригонометрическая, кусочно-сплайновая и др.), но наиболее употребительна интерполяция полиномами. Полиномом называют функцию вида 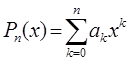. Здесь наивысшая степень n называется порядком полинома. Полином легко вычисляется (например, по схеме вычисления Горнера), дифференцируется и интегрируется. Ищем интерполирующую функцию в виде полинома Ln(x).

Запишем условие близости интерполяции:

- система уравнений первой степени для величин , где полином выражен формулой и -неизвестные коэффициенты, которые необходимо определить, а - степени узлов интерполяции (узлы заданы по условию).

Для 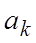получаем систему линейных уравнений 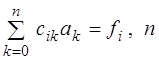-степень полинома, 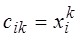, где 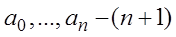неизвестный коэффициент.

Дата добавления: 2015-07-11