Балансовые модели

Матричные (балансовые) модели представляют собой математическое выражение балансового метода планирования (метод взаимного сопоставления затрат и результатов).

Матричные модели объединяют общий принцип построения, единство системы расчётов и аналогичность ряда экономических характеристик.

В качестве примера указанных моделей в данной главе рассматриваются статическая и динамическая модели межотраслевого стоимостного баланса, межпродуктовый баланс для обеспечения взаимоувязки планов производства группы предприятий или обособленных подразделений (цехов, бригад, иных структур) одной организации.

Основное внимание при этом уделяется структуре и экономической интерпретации элементов статических моделей.

Межотраслевой баланс отражает производство и распределение валового национального продукта по отраслям, межотраслевые потоки, использование материальных и трудовых ресурсов, создание и распределение национального дохода.

Экономико-математическая модель межотраслевого баланса представляет собой систему уравнений, отражающих функциональную взаимосвязь включённых в его систему элементов:

где — вектор валовой продукции,

— вектор конечной продукции (конечное потребление и накопление),

— производственные (материальные) затраты й отрасли в течение планового периода, допустим, года (например, если отрасль 1 — угольная, отрасль 2 — чёрная металлургия, то — годовые затраты угля на производство чёрных металлов).

С учётом обозначений

система уравнений перепишется в виде:

или в более компактном виде: (запись с использованием знаков суммирования),

либо 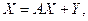где — вектор валовой продукции, — вектор конечной продукции;

— матрица прямых (материальных) затрат.

Именно в этих двух формах записи, как правило, и используется экономико-математическая модель межотраслевого баланса, которую называют моделью Леонтьева или моделью «затраты - выпуск».

Элементы матрицы 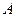называют коэффициентами прямых затрат —это затраты 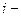й отрасли на единицу (рубль) валовой продукции й отрасли.

В матричной форме модель Леонтьева можно записать в виде или .

Последнее соотношение можно использовать для анализа и планирования решения следующих задач:

1) определения объёмов конечного продукта отраслей по заданным объёмам валовой продукции ;

2) определение объёмов валовой продукции по заданным объёмам конечной продукции .

Кроме того, можно определить величины конечной продукции части отраслей и объёмы валовой продукции других отраслей, если задать для первых отраслей величины валовой продукции, а для всех остальных отраслей задать объёмы конечной продукции.

Элементы обратной матрицы 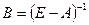называются коэффициентами полных (материальных) затрат — это затраты 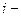й отрасли на каждый рубль конечной продукции отрасли . Соответственно матрицу В называют матрицей полных затрат.

Неотрицательную матрицу 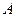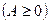называют продуктивной, если существует хотя бы один такой положительный вектор , что .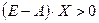

Это определение имеет простой экономический смысл: матрица 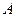продуктивна, если существует такой план , что каждое производственное подразделение (отрасль, предприятие, цех) может произвести некоторое количество конечной продукции.

Имеет место замечательный факт, что продуктивность матрицы является необходимым и достаточным условием существования, единственности и неотрицательности решения системы уравнений 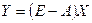при любом неотрицательном векторе .

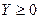Укажем некоторые способы определения продуктивности матрицы 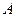(признаки продуктивности): для её продуктивности необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий.

1. Матрица неотрицательно обратима, т.е. существует обратная матрица 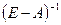и все её элементы неотрицательны.

2. Положительны все главные миноры матрицы .

3. Максимальное собственное число матрицы 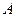меньше единицы — (собственными значениями (числами) квадратной матрицы 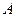называются корни (решения) характеристического уравнения

Пример

Предприятие выпускает продукцию трёх видов, причём каждое из его структурных подразделений (цехов) специализируется на выпуске только одного вида: первый цех выпускает продукцию первого вида, второй — продукцию второго вида, третий — продукцию третьего вида. Часть продукции идёт на внутреннее потребление, остальная является конечным продуктом.

Имеются экономические оценки коэффициентов прямых затрат и объёмов конечной продукции:

Требуется оценить продуктивность матрицы 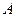прямых затрат и составить баланс производства и распределения продукции предприятия.

Решение.

Оценим продуктивность матрицы 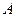по всем трём вышеприведённым признакам

1. Вычислим

Поскольку все элементы матрицы 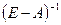неотрицательны, то по первому признаку матрица 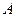продуктивна.

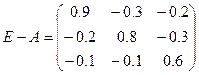
2. Определим все главные миноры матрицы :

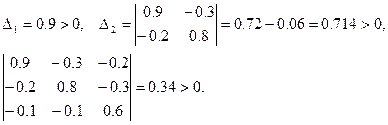
Поскольку все главные миноры положительны, то по второму признаку матрица 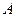продуктивна.

3. Используя инструмент «Подбор параметра» находим собственные числа матрицы 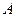. Это 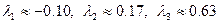. Поскольку максимальное из собственных чисел 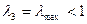, то по третьему признаку матрица 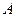продуктивна.

Рис.1

Модель баланса производства и распределения продукции предприятия можно представить следующей системой линейных уравнений:

(1)

Решение системы (1) можно записать в виде:

(2)

Формула (2) позволяет определить валовую продукцию цехов.

Введём обозначения:

— валовая продукция i-го цеха, причём

Вычислим вектор Х валовой продукции предприятия.

Дата добавления: 2015-07-11