
Читайте также:
|
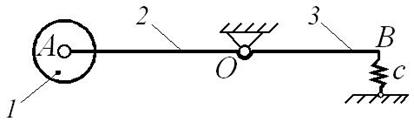
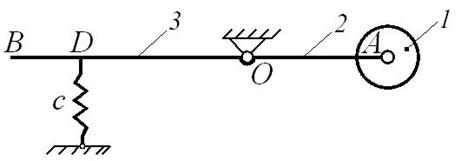
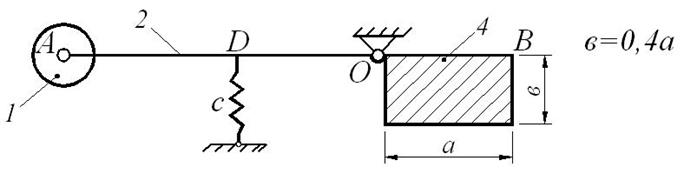
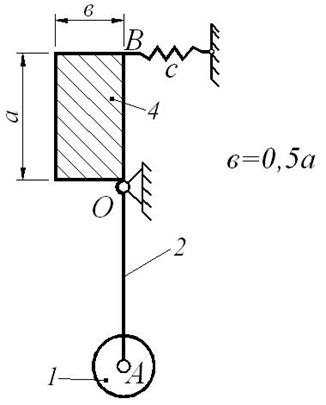
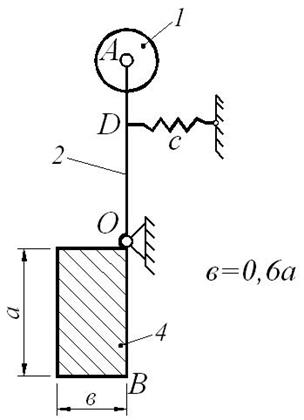
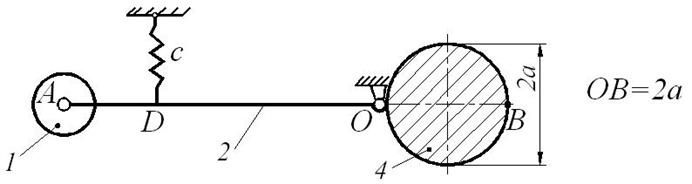
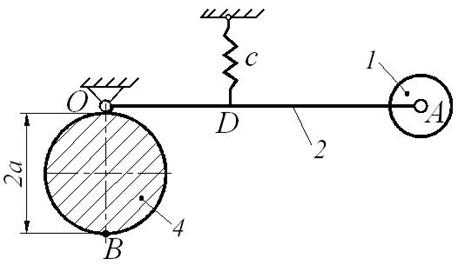
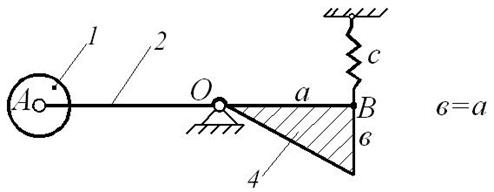
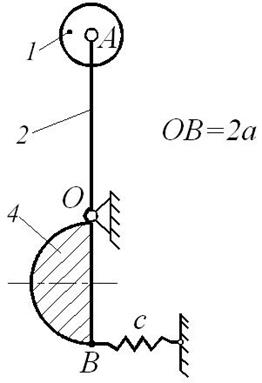
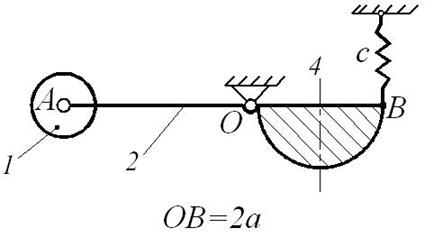
Составить дифференциальное уравнение малых колебаний механической системы, показанной на рис. Д10.1, около ее положения равновесия и найти период этих колебаний. Известны массы: m 1 груза А, m 2 стержня ОА, m 3 стержня ОВ и m 4 плоской фигуры (прямоугольника, круга, полукруга или треугольника). Жесткость пружины с (Н/м). Размеры: l 2 – длина стержня ОА, l 3 – длина стержня ОВ, d – длина участка OD (схемы 1, 2, 4, 5 и 6), также как и массы, приведены в таблице Д10-1.
Массами пружины и стержня ОВ (на схемах 2-9), а также размерами груза А пренебречь.
На схемах (рис. Д10.1) показано положение равновесия механической системы.
При малых отклонениях системы от положения равновесия можно считать, что пружина остается вертикальной (схемы 0, 1, 2, 5, 6, 7 и 9) или горизонтальной (схемы 3, 4 и 8).
Указания: 1. Номер схемы на рис. Д10.1 выбирается в соответствии с последней цифрой шифра (зачетной книжки).
2. Данные из табл. Д10-1 выбирать согласно предпоследней цифре шифра.
|
|
|
|
|
|
|
|
|
|
Рис. Д10.1
Таблица Д10-1
| Предпоследняя цифра шифра | m 1 | m 2 | m 3 | m 4 | l 2 | l 3 | d | c, Н/м |
| кг | м | |||||||
| 0,5 | 0,40 | 0,15 | ||||||
| 0,6 | 0,48 | 0,20 | ||||||
| 0,7 | 0,56 | 0,23 | ||||||
| 0,8 | 0,64 | 0,27 | ||||||
| 0,9 | 0,72 | 0,30 | ||||||
| 1,0 | 0,80 | 0,33 | ||||||
| 1,1 | 0,88 | 0,36 | ||||||
| 1,2 | 0,96 | 0,40 | ||||||
| 1,3 | 1,04 | 0,43 | ||||||
| 1,4 | 1,12 | 0,46 |
Дата добавления: 2015-07-11; просмотров: 112 | Нарушение авторских прав