Уравнение Лагранжа ΙΙ рода.

Содержание

стр.

1. Уравнение Лагранжа ІІ рода……………………………………………………...

1.1. Обобщенные координаты и обобщенные скорости……………………………

1.2. Обобщенные силы………………………………………………………………….

1.3. Условия равновесия системы в обобщенных координатах……………………

1.4. Об устойчивости равновесия консервативной механической системы………...

1.5. Уравнение Лагранжа……………………………………………………………….

2. Методика решения задач……………………………………………………………

3. Свободные колебания системы с одной степенью свободы………………...……

4. Задание Д9. Применение уравнения Лагранжа ІІ рода для изучения движения механической системы………………………………………………………………

5. Пример выполнения задания Д9……………………………………………………

6. Задание Д10. Применение уравнения Лагранжа ІІ рода для исследования малых колебаний механической системы с одной степенью свободы………………………….……………………………………………………

7. Пример выполнения задания Д10...…………………………………………….......

8. Приложение 1. Задание Д8. Применение общего уравнения динамики для изучения движения механической системы……………………………………….

9. Приложение 2. Осевые моменты инерции однородных плоских фигур………...

Литература

Уравнение Лагранжа ΙΙ рода.

1.1. Обобщенные координаты и обобщенные скорости.

Обобщенными или лагранжевыми координатами данной механической системы называются такие независимые друг от друга параметры любой размерности, при помощи которых можно в любой момент определить положение этой системы и, следовательно, выразить декартовы координаты всех ее точек через эти параметры.

Число независимых обобщенных координат механической системы, подчиненной идеальным и голономным связям, равно числу степеней свободы.

Так, кривошипно-шатунный механизм является системой с одной степенью свободы. В качестве обобщенной координаты может быть выбран угол поворота кривошипа, значением которого однозначно определяются положения всех материальных точек данного механизма (данной механической системы).

Положение свободной материальной точки в пространстве определяется тремя декартовыми координатами, не зависящими друг от друга. Поэтому свободная материальная точка имеет три степени свободы, и в качестве обобщенных целесообразно принять декартовы координаты.

Положение твердого тела, вращающегося вокруг неподвижной оси однозначно определяется углом поворота этого тела. Следовательно, данное тело имеет одну степень свободы и обобщенной координатой является угол поворота тела.

Как видно, в качестве обобщенных координат можно выбирать параметры, имеющие любую размерность: линейную, угловую, площади и т.д.

В этом пособии будем рассматривать механические системы с одной степенью свободы.

Условимся обозначать обобщенную координату буквой q.

Следовательно, для кривошипно-шатунного механизма обобщенная координата q = φ.

При движении механической системы с одной степенью свободы ее обобщенная координата будет с течением времени непрерывно изменяться. Закон этого движения определится уравнением:

которое представляет собой кинематическое уравнение движения системы в обобщенных координатах.

Производная от обобщенной координаты по времени называется обобщенной скоростью механической системы. Будем обозначать обобщенную скорость символом 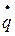, где . Размерность обобщенной скорости зависит от размерности обобщенной координаты. Если q – линейная величина, то 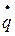- линейная скорость; если q – угол, то 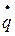- угловая скорость; если q – площадь, то 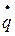- секторная скорость и т.д. Как видим, понятием об обобщенной скорости охватываются все встречавшиеся ранее в кинематике понятия о скоростях.

1.2. Обобщенные силы

Обобщенной силой Q, соответствующей обобщенной координате q, называют скалярную величину, определяемую отношением элементарной работы заданных сил, на перемещении механической системы, вызванном элементарным приращением δq координаты q, к величине этого приращения, т.е.

Размерность обобщенной силы зависит от размерности обобщенной координаты. Так как

то размерность обобщенной силы равна размерности работы, деленной на размерность соответствующей обобщенной координаты. Отсюда видно, что если q – линейная величина, то Q имеет размерность силы (в системе СИ – Н или кН); если q – угол (измеряется в радианах), то Q будет измеряться в Н·м, т.е. имеет размерность момента; если q – объем (например, положение поршня в цилиндре можно определить объемом запоршневого пространства), то Q будет измеряться в Н/м², т.е. имеет размерность давления, и т.д. Как видим, по аналогии с обобщенной скоростью, понятием об обобщенной силе охватываются все величины, встречавшиеся ранее как меры механического взаимодействия материальных тел (сила, момент, давление).

Случай потенциальных сил. Если все действующие на систему силы потенциальны, то обобщенная сила равна взятой со знаком минус частной производной от потенциальной энергии по соответствующей обобщенной координате, т.е.

1.3. Условия равновесия системы в обобщенных координатах.

Согласно принципу возможных перемещений необходимым и достаточным условием равновесия механической системы является равенство нулю суммы элементарных работ всех заданных сил (и сил трения, если они совершают работу) на любом возможном перемещении системы, т.е.

В обобщенных координатах для механической системы с одной степенью свободы это условие дает

Так как элементарное приращение обобщенной координаты , то для равновесия механической системы с одной степенью свободы необходимо и достаточно, чтобы обобщенная сила, соответствующая выбранной обобщенной координате, была равна нулю:

(1)

Случай потенциальных сил. В этом случае условие равновесия (1) дает

Отсюда следует, что при равновесии полный дифференциал функции П равен нулю, т.е.

Таким образом, механическая система, на которую действуют потенциальные силы, находится в равновесии в тех положениях, для которых потенциальная энергия системы имеет экстремум (в частности, минимум или максимум).

1.4. Об устойчивости равновесия консервативной механической системы

Рассмотрим механическую систему с голономными и стационарными связями, имеющую одну степень свободы и находящуюся под действием сил, имеющих потенциал. Такую систему материальных точек называют консервативной. Уравнение равновесия в обобщенных координатах имеет вид:

Q = 0. (а)

Так как в случае консервативных сил

(б)

то для консервативной системы уравнение равновесия (а) принимает вид:

(в)

Отсюда следует, что положениями равновесия рассматриваемой системы в случае консервативных сил являются те положения, при которых потенциальная энергия этой системы принимает экстремальные значения. Однако, уравнение (в) не устанавливает, являются ли рассматриваемые равновесные положения системы устойчивыми или неустойчивыми.

Условия устойчивости равновесия системы с конечным числом степеней свободы устанавливаются следующей теоремой Лагранжа-Дирихле: равновесные положения консервативной системы, в которых ее потенциальная энергия достигает минимума, устойчивы.

Равновесное положение консервативной системы является устойчивым, если система, равновесие которой нарушено малым отклонением и малой начальной скоростью , совершает малые колебания около этого равновесного положения.

Теорема Лагранжа-Дирихле устанавливает, что равновесие механической системы, находящейся под действием консервативных сил, является устойчивым, если в этом положении ее потенциальная энергия имеет минимум.

Для системы с одной степенью свободы существование минимума потенциальной энергии в положении равновесия определяется следующим условием:

(г)

Это уравнение используют при решении задач на устойчивость равновесия системы с одной степенью свободы.

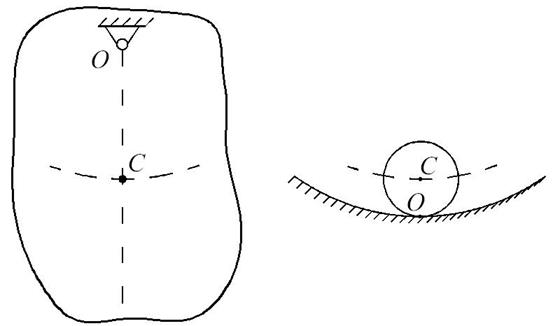
Рис. 1

Рис. 2

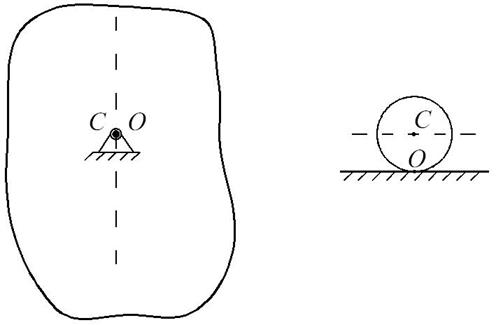
Рис. 3

На рис. 1 изображены равновесные положения физического маятника и шарика, при которых их центры тяжести занимают найнизшие положения по отношению к точке О. В этих положениях потенциальная энергия тел имеет минимум и равновесие является устойчивым.

На рис. 2 центры тяжести физического маятника и шарика занимают наивысшие положения. При этом потенциальная энергия тел имеет максимум и равновесие является неустойчивым.

В положениях, изображенных на рис. 3, физический маятник и шарик находятся в положении безразличного равновесия.

1.4. Уравнение Лагранжа

Дифференциальное уравнение движения механической системы в обобщенных координатах или уравнение Лагранжа имеет вид

(2)

где: Т – кинетическая энергия механической системы;

q – обобщенная координата;

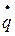- обобщенная скорость;

Q – обобщенная сила, соответствующая выбранной обобщенной координате.

В общем случае, для исследования механической системы с «n» степенью свободы необходимо составлять n уравнений Лагранжа.

Уравнения Лагранжа дают единый и при том достаточно простой метод решения задач динамики. Важное преимущество этих уравнений состоит в том, что их вид и число не зависят ни от количества тел (или точек), входящих в рассматриваемую систему, ни от того, как эти тела движутся; число уравнений Лагранжа определяется только числом степеней свободы системы. Кроме того, при идеальных связях в правые части уравнения (2) входят обобщенные заданные (активные) силы, и, следовательно, уравнения Лагранжа позволяют заранее исключить из рассмотрения все наперед неизвестные реакции связей.

Основная задача динамики в обобщенных координатах состоит в том, чтобы зная обобщенную силу Q и начальные условия, найти закон движения системы в виде , т.е. определить обобщенную координату как функцию времени. Так как кинетическая энергия T зависит от обобщенной скорости 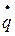, то при дифференцировании первого члена уравнения (2) по t в левой части этого уравнения появляется вторая производная по времени от искомой координаты. Следовательно, уравнение Лагранжа представляет собой обыкновенное дифференциальное уравнение второго порядка относительно обобщенной координаты q.

Случай потенциальных сил. Если все действующие на механическую систему силы потенциальные, то уравнение (2) можно представить в виде:

(3)

или

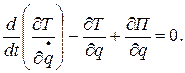(4)

Введем функцию

(5)

Функция L от обобщенных координат и обобщенных скоростей, равная разности между кинетической и потенциальной энергиями системы, называется функцией Лагранжа или кинетическим потенциалом. Тогда, в случае потенциальных сил уравнение (4) с учетом (5):

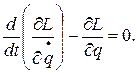(6)

Уравнение (6) справедливо потому, что потенциальная энергия П зависит только от обобщенной координаты q, а от обобщенной скорости 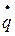не зависит.

Из полученного результата (6) следует, что состояние механической системы, на которую действуют потенциальные силы, определяется заданием одной только функции Лагранжа, так как, зная эту функцию, можно составить дифференциальные уравнения движения механической системы.

Дата добавления: 2015-07-11