Решение. 1. Для решения задачи воспользуемся уравнением Лагранжа II рода:

1. Для решения задачи воспользуемся уравнением Лагранжа II рода:

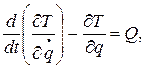
где: T – кинетическая энергия механической системы;

q – обобщенная координата;

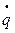- обобщенная скорость;

Q – обобщенная сила.

Предполагаем, что движение механической системы таково, при котором груз 1 опускается по наклонной плоскости.

Данная механическая система имеет одну степень свободы. В качестве обобщенной координаты выберем координату х, определяющую положение груза 1, отсчитываемую от центра О (см. рис. Д9.1). Тогда q = х, а .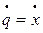

2. Определение кинетической энергии механической системы.

Кинетическая энергия механической системы равна сумме кинетических энергий тел системы:

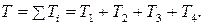
Кинетическая энергия груза 1, совершающего поступательное движение:

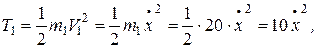Н·м.

Кинетическая энергия блока 2 равна нулю потому, что его масса равна нулю, т.е.

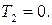
Кинетическая энергия блока 3, совершающего вращательное движение, равна:

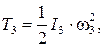
где: I ₃ – момент инерции блока 3 относительно оси вращения;

ω₃ – угловая скорость блока 3.

Момент инерции блока 3 определим, зная массу и радиус инерции этого тела:

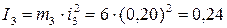кг·м².

Угловую скорость блока 3 выразим через линейную скорость 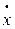груза 1:

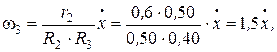с^-1.

Следовательно,

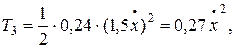Н·м.

Кинетическая энергия катка 4, совершающего плоское движение, равна:

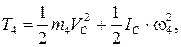
где: V_C – скорость центра масс катка (т. С);

I_С – момент инерции катка относительно оси, проходящей через центр масс;

ω₄ – угловая скорость вращения катка.

Выразим скорости V_C и ω₄ через скорость 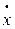груза 1:

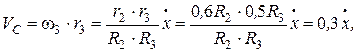м/с;

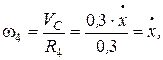с^-1.

Момент инерции катка:

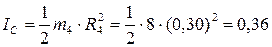кг·м².

Кинетическая энергия катка:

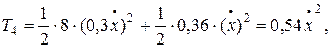Н·м.

Таким образом, кинетическая энергия системы равна:

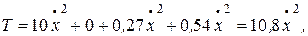Н·м.

3. Продифференцируем значение кинетической энергии Т в соответствии с уравнением Лагранжа:

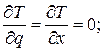
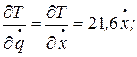
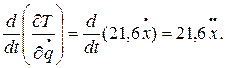
4. Определим обобщенную силу Q, соответствующую обобщенной координате х. Для этого дадим системе положительное приращение δ х и определим сумму элементарных работ всех заданных сил, действующих на систему, на перемещении δ х. К заданным силам добавим силу трения 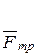(вследствие трения скольжения груза 1 о наклонную плоскость) и момент сопротивления 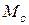, имеющий место вследствие трения качения катка при его движении по плоскости, размещенной под углом β к горизонтали.

При перемещении груза на δ х блок 2 повернется на угол δφ₂, блок 3 – на угол δφ₃, каток 4 повернется на угол δφ₄, а его центр масс переместится на δ S_C. Выразим эти перемещения через δ х:

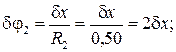
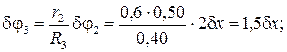
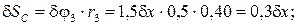
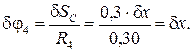
Сумма элементарных работ всех заданных сил равна:

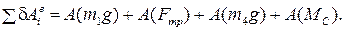
Элементарная работа силы тяжести m ₃ g равна нулю, т.к. эта сила приложена к неподвижной точке.

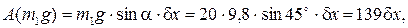Н·м;

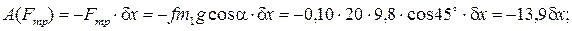
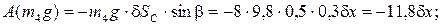
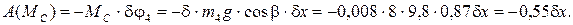
Следовательно,

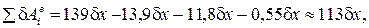Н·м.

Обобщенная сила:

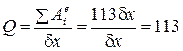Н.

Подставляем полученные результаты в уравнение Лагранжа II рода:

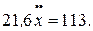
Таким образом, ускорение груза 1:

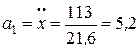м/с².

Ускорение т. С определим, дважды дифференцируя по времени уравнение δ S_C = 0,3 δ x:

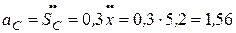м/с².

Ответ: 1. Груз 1 движется по наклонной плоскости вниз.

2. а ₁ = 5,2 м/с²; а _С = 1,56 м/с².

Дата добавления: 2015-07-11