Свободные колебания системы с одной степенью свободы

Механическая система называется системой с одной степенью свободы, если ее положение в пространстве может быть однозначно определено заданием одной величины q, называемой обобщенной координатой. Движение системы в пространстве при этом определяется зависимостью обобщенной координаты от времени.

Принимая положение устойчивого равновесия за начало отсчета обобщенной координаты и за нулевой уровень потенциальной энергии, рассмотрим малые движения системы около положения устойчивого равновесия. Отклонение системы от положения равновесия при таком выборе начала отсчета будет определяться значением обобщенной координаты.

Полагая, при составлении дифференциальных уравнений малых движений обобщенные координаты (отсчитываемые от положения равновесия) и обобщенные скорости малыми величинами, ограничимся в дифференциальных уравнениях движения линейными членами. Этот прием, заключающийся в отбрасывании в нелинейных дифференциальных уравнениях членов, содержащих квадрат и более высокие степени обобщенных координат и скоростей, называется линеаризацией уравнений. Такая линеаризация, естественно, в известной мере искажает действительную картину движений, однако, чем меньше отклонения системы от положения устойчивого равновесия, тем точнее линеаризованные уравнения будут описывать движение системы. Линеаризация дифференциальных уравнений позволяет получить замкнутое решение для таких систем, для которых нахождение интегралов точной, нелинейной системы уравнений в конечном виде, как правило, невозможно.

Удобным способом составления дифференциальных уравнений малых колебаний системы является использование уравнений Лагранжа в виде (2) или (3).

Кинетическая энергия системы, подчиненной стационарным связям, выражается через обобщенные координаты и скорости формулой:

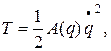
где А(q) является положительной функцией координаты q. Пренебрегая квадратом и более высокими степенями q и 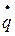, приближенно принимаем

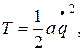(7)

где а – всегда положительный инерционный коэффициент. Для линейных обобщенных координат этот инерционный коэффициент имеет размерность массы, для угловых координат – размерность момента инерции твердого тела относительно оси.

Потенциальная энергия системы является функцией обобщенной координаты. Отбрасывая члены порядка выше второго, имеем:

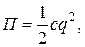(8)

где постоянная с называется квазиупругим коэффициентом.

Внося значения кинетической (7) и потенциальной (8) энергий в уравнение Лагранжа (3), взяв соответствующие производные, получаем дифференциальное уравнение малых свободных колебаний системы с одной степенью свободы:

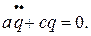(9)

Это уравнение имеет структуру, аналогичную дифференциальному уравнению свободных колебаний материальной точки, возникающих под действием линейной восстанавливающей силы. Общий интеграл этого уравнения имеет вид:

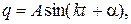(10)

где: А – амплитуда колебаний;

k – частота колебаний;

α – начальная фаза;

kt + α – фаза колебаний.

Частота колебаний зависит от значений инерционного и квазиупругого коэффициентов:

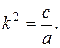
Амплитуда и начальная фаза колебаний определяются по начальным условиям. Обозначая начальные значения обобщенной координаты и ее производной при t = 0 через q = q ₀ и 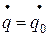, имеем:

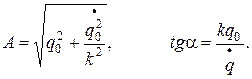
Период колебаний:

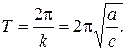
Свободные, или, иначе, собственные колебания системы, определяемые уравнением (10), являются гармоническими колебаниями. Их частота и период не зависят от начальных условий – это свойство называется изохронностью малых колебаний.

При решении задач на свободные колебания системы с одной степенью свободы рекомендуется следующий порядок действий:

1) выбираем обобщенную координату q;

2) определяем кинетическую энергию системы как функцию квадрата обобщенной скорости ;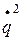

3) находим значение потенциальной энергии системы;

4) внося эти величины в уравнение Лагранжа, получаем дифференциальное уравнение малых колебаний;

5) интегрируя это уравнение и определяя произвольные постоянные интегрирования, находим уравнение движения системы;

6) определяем период колебаний и другие искомые параметры.

Дата добавления: 2015-07-11