Пример решения задания Д10.

Условие задачи в кратком виде:

Дано: m ₁ = 40 кг; m ₂ = 25 кг; m ₄ = 60 кг; ОА = l ₂ = 1,5 м; OD = d = 1,0 м; OB = 2 a = = 1,2 м; с = 7000 Н/м; схема – на рис. Д10-2. _________________________

Найти: 1) дифференциальное уравнение малых колебаний -?

2) Т -?

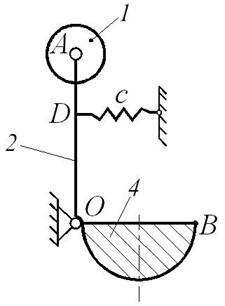
Рис. Д10.2

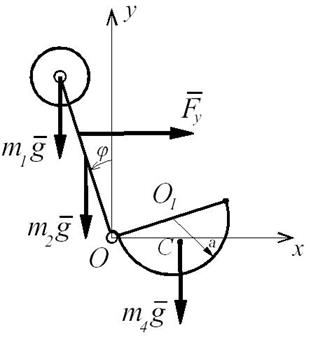
Рис. Д10.3

Решение.

На рис. Д10-2 показана механическая система в положении устойчивого равновесия.

Покажем систему в произвольном положении (рис. Д10-3). За обобщенную координату данной системы с одной степенью свободы принимаем угол φ отклонения стержня ОА от вертикали, отсчитываемый против направления движения часовой стрелки, т.е.

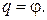
Обобщенная скорость 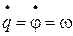, т.е. обобщенная скорость – угловая скорость вращения механической системы относительно оси Z (на рис. не показана), проходящей через опору О.

Запишем уравнение Лагранжа (учитываем, что все заданные силы потенциальные):

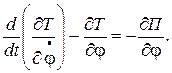
Вычисляем кинетическую энергию системы:

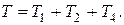
Кинетическая энергия груза 1, который принимаем за материальную точку:

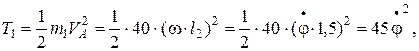Н·м.

Кинетическая энергия стержня ОА, вращающегося вокруг точки О:

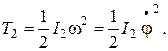
Момент инерции стержня ОА относительно оси вращения:

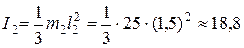кг·м².

Следовательно,

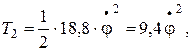Н·м.

Кинетическая энергия плоской фигуры 4 (полукруга) относительно оси вращения О:

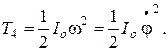
Момент инерции плоской фигуры относительно оси вращения О определим при помощи теоремы Гюйгенса-Штейнера:

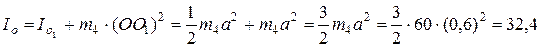кг·м².

где: 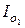- момент инерции полукруга относительно оси, проходящей через т. О₁.

Получаем:

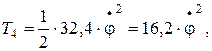Н·м.

Таким образом, кинетическая энергия системы равна:

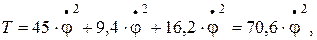Н·м.

Продифференцируем выражение кинетической энергии:

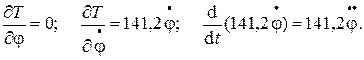
Вычислим потенциальную энергию системы. За нулевое положение системы примем ось ох.

Потенциальная энергия силы тяжести :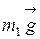

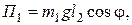Н·м;

Потенциальная энергия силы тяжести :

Н·м;

Потенциальная энергия силы тяжести :

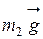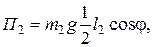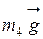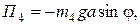Н·м;

Потенциальная энергия силы упругости:

где: λ – удлинение пружины, причем

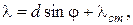
где: λ_ст – статическое сжатие пружины в положении равновесия.

Таким образом, потенциальная энергия системы равна:

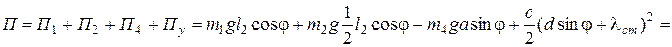
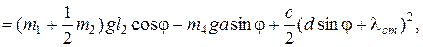Н·м;

Частная производная от потенциальной энергии П по обобщенной координате φ равна:

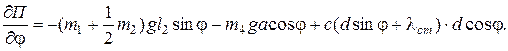
В положении равновесия система сумма моментов всех сил относительно точки О равна нулю. Следовательно:

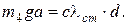
Поэтому:

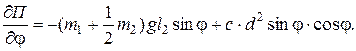
При малых колебаниях механической системы около положения равновесия ввиду незначительности угла φ можно положить:

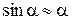и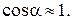

Тогда

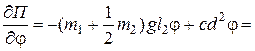
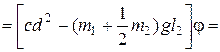
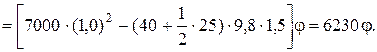
Уравнение Лагранжа будет иметь вид:

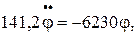
или

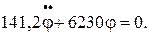
Обозначим

Таким образом получим дифференциальное уравнение свободных колебаний:

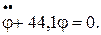
Период колебаний

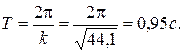
Ответ: 1)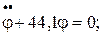

2)

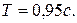
Дата добавления: 2015-07-11