Методика решения задач

Уравнениями Лагранжа можно пользоваться для изучения движения любой механической системы с геометрическими* связями, независимо от того, сколько тел входит в систему, как движутся эти тела и какое движение (абсолютное или относительное) рассматривается.

Чтобы для данной механической системы составить уравнения Лагранжа, надо:

1) установить число степеней свободы системы и выбрать обобщенные координаты (для механической системы с одной степенью свободы выбрать одну обобщенную координату);

2) изобразить систему в произвольном положении и показать на рисунке все заданные силы (если связи неидеальные, то необходимо учесть и силы трения);

  * геометрические связи – связи, налагающие ограничения на положения точек системы в пространстве, но не на их скорости

3) вычислить обобщенную силу Q; при этом, во избежание ошибок в знаках, сообщаемое системе возможное перемещение должно быть направлено так, чтобы приращение обобщенной координаты было положительным;

4) вычислить кинетическую энергию системы в ее абсолютном движении и выразить эту энергию через обобщенную скорость ;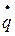

5) подсчитать соответствующие частные производные от T по q и 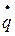и подставить все вычисленные параметры в уравнение Лагранжа.

Из полученных уравнений, если заданы действующие силы и начальные действия, можно, интегрируя эти уравнения, найти закон движения системы в виде . Если же задан закон движения, то составленные уравнения позволяют определить заданные силы.

Когда все приложенные к системе силы потенциальные, уравнение Лагранжа можно составлять в виде (3) или (6). При этом, вместо вычисления обобщенной силы надо определить потенциальную энергию системы, выразив ее через обобщенную координату, и затем, взяв производную от П по обобщенной координате, подставить в уравнение (3). При необходимости можно составить функцию Лагранжа и воспользоваться уравнением (6).

Дата добавления: 2015-07-11