
Читайте также:
|
Рассмотрим однородный стержень длины  , теплоизолированный с боков и Д. тонкой, чтобы в любой момент времени температуру во всех точках поперечного сечения м.б. считать одинаковой. Процесс распространения температуры в стержне м.б. описан функцией
, теплоизолированный с боков и Д. тонкой, чтобы в любой момент времени температуру во всех точках поперечного сечения м.б. считать одинаковой. Процесс распространения температуры в стержне м.б. описан функцией  имеет вид
имеет вид  - уравнение теплопроводности, где
- уравнение теплопроводности, где  - плотность теплового потока, равная количеству тепла, протекшего в единицу времени ч/з площадь в/см^2, c –удельная теплоемкость,
- плотность теплового потока, равная количеству тепла, протекшего в единицу времени ч/з площадь в/см^2, c –удельная теплоемкость,  - плотность.
- плотность. 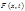 - плотность тепловых источников в точке х в момент t. В частности, если стержень однороден, то уравнение теплопроводности:
- плотность тепловых источников в точке х в момент t. В частности, если стержень однороден, то уравнение теплопроводности:  , если источники отсутствуют, т.е.
, если источники отсутствуют, т.е. 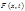 =0, то уравнение теплопроводности
=0, то уравнение теплопроводности 
1) Постановка краевых задач.
Для выделения единого решения уравнения теплопроводности Н. к уравнению присоединить начальные и граничные условия. Начальное условие состоит в задании значений функции  в начальный момент
в начальный момент 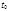 .
.
Рассмотрим 3 основных типа граничных условий.
1)На конце стержня x=0 задана температура  , где
, где  - функция, заданная в некоторых промежутке
- функция, заданная в некоторых промежутке  , T – промежуток времени, в течении которого изучается процесс.
, T – промежуток времени, в течении которого изучается процесс.
2) На конце  , задано значение производной
, задано значение производной  .
.
3) На конце  задано линейное соотношение м/ду производной и функцией.
задано линейное соотношение м/ду производной и функцией.
 , где
, где  - коэффициент теплообмена,
- коэффициент теплообмена,  - некоторая функция.
- некоторая функция.
Первая краевая задача состоит в отыскании решения  уравнения теплопроводности
уравнения теплопроводности  при
при  , удовлетворяющего условиям:
, удовлетворяющего условиям:

 , где
, где 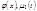 и
и  - заданные функции.
- заданные функции.
Аналогично ставятся и другие краевые задачи с различными комбинациями краевых условий при x=0 и  .
.
Первая краевая задача для полубесконечного стержня.
Найти решение уравнения теплопроводности в области  и
и  , удовлетворяющее условиям
, удовлетворяющее условиям 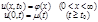
2) Метод разделения переменных.
Рассмотрим первую краевую задачу для уравнения теплопроводности на отрезке: 
 (1) с начальными условиями
(1) с начальными условиями  (2) и граничными условиями
(2) и граничными условиями  (3)
(3)
Для решения этой задачи рассматривают, как принято в методе разделения переменных, сначала основную вспомогательную задачу:
Найти решение уравнения  , не равное тождественно нулю, удовлетворяющее однородным граничным условиям
, не равное тождественно нулю, удовлетворяющее однородным граничным условиям  (3`) и представимое в виде
(3`) и представимое в виде  , (4) где
, (4) где  - функция только переменного x,
- функция только переменного x, 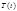 - функция только переменного t.
- функция только переменного t.
Подставляя (4) в (1) и производя деление обеих частей равенства на  , получим:
, получим:
 , т.к. левая часть зависит только от t, правая - от х.
, т.к. левая часть зависит только от t, правая - от х.
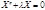 ,(5)
,(5)  (5`)
(5`)
Граничные условия (3`) дают: 
Т.о. для определения функции X(x) получим задачу о собственных значен. (Штурма - Лиувилля) 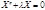 ,
,  (6)
(6)
Известно, что только для значений параметра  , равных
, равных  (7) существует нетривиальное решение уравнения (5), равные
(7) существует нетривиальное решение уравнения (5), равные  (8)
(8)
Этим значениям  соответствуют решения уравнения (5`)
соответствуют решения уравнения (5`)
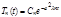 (9)
(9)
Функции  (10) является частными решениями уравнения (1), удовлетворяющими нулевым граничным условиям
(10) является частными решениями уравнения (1), удовлетворяющими нулевым граничным условиям
Составим ряд  (*)
(*)
Функция  удовлетворяет граничным условиям, т.к. им удовлетворяют все члены ряда. Требуя выполнения начальных условий, получаем:
удовлетворяет граничным условиям, т.к. им удовлетворяют все члены ряда. Требуя выполнения начальных условий, получаем:
 (11), т.е.
(11), т.е.  является коэффициентами Фурье функции
является коэффициентами Фурье функции  при разложении её в ряд по синусам на интервале
при разложении её в ряд по синусам на интервале 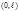 :
:
 (12)
(12)
Т.о., ряд (*) с коэффициентами  , определенными по формуле (12) удовлетворяет всем условиям искомой задачи и является решением задач (1),(2),(3).
, определенными по формуле (12) удовлетворяет всем условиям искомой задачи и является решением задач (1),(2),(3).
Дата добавления: 2015-07-11; просмотров: 275 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В.13. Задача Коши для уравнения колебания струны. Формула Даламбера. | | | ЗАДАЧА № 2-1 |