Эксцентриситет гиперболы

Рассмотрим гиперболу с фокусами в точках F₁ и F₂ , действительной осью которой является [A₁A₂].

Определение. Эксцентриситетом гиперболы называется число, равное .

Так как , то ε > 1. Пусть гипербола задана уравнением 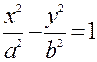, тогда => => 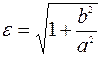. => Эксцентриситет определяется отношением полуосей гиперболы. Чем меньше эксцентриситет гиперболы, тем меньше углы, образуемые асимптотами, в которых лежит гипербола и тем больше гипербола «вытягивается» вдоль своей действительной оси. Рис.10

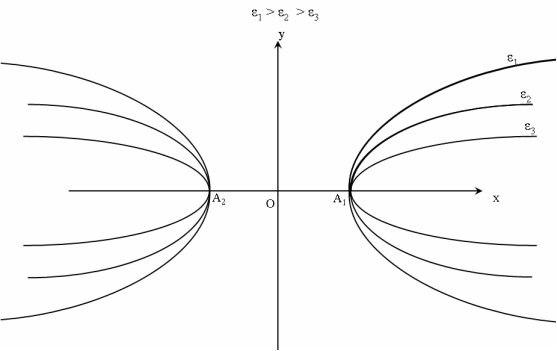
Рис.10.

5.Построение точек гиперболы

Если для гиперболы заданы положения её вершин A₁ , A₂ и фокусов F₁, F₂, то её можно построить следующим образом:

а) Строим окружность ω₁(F₁,R₁) с центром в правом фокусе F₁ произвольным радиусом R₁.

б) Строим окружность ω₂(F₂,R₂) с центром в левом фокусе F₂ радиусом R₂ = R₁+[A₁A₂].

в) В этом случае точка М =ω₁ ∩ ω₂ принадлежит гиперболе, так как для этой точки ||F₁M| ─|F₂M|| = |A₁A₂| =2a.

Повторяя, построения а), б) и в) несколько раз можно получить необходимое число точек для построения правой ветви гиперболы.

Рис.11.

Левую ветвь гиперболы можно построить аналогично, поменяв фокусы F₁ и F₂ местами.

Дата добавления: 2015-07-11