Исследование формы гиперболы по ее уравнению

1. Уравнение содержит х и у только в четных степенях. Следовательно, гипербола симметрична относительно осей Ох и Оу, а также относительно точки О (0; 0), которую называют центром гиперболы.

2. Найдем точки пересечения гиперболы с осями координат. Положив у = 0 в уравнении , находим две точки пересечения гиперболы с осью Ox:. A₁ (a;0) и А₂(-а;0). Положив х = 0, получаем у² = - b ², чего быть не может. Следовательно, гипербола ось Оу не пересекает.

Точки A₁ (a;0) и А₂(-а;0) называются вершинами гиперболы, аотрезок А₁А₂ = 2а — действительной осью, отрезок ОА₁ = ОА₂ = а - действительной полуосью гиперболы.

Отрезок В₁В₂ (В₁В₂ = 2 b), соединяющий точки B₁ (0; b) и В₂(0; - b) называется мнимой осью, число b — мнимой полуосью. Прямоугольник со сторонами 2 а и 2 b называется основным прямоугольником гиперболы.

3. Из уравнения следует, что уменьшаемое не меньше единицы, т. е. что ≥ 1 или |х| ≥ а. Это означает, что точки гиперболы расположены справа от прямой х = а (правая ветвь гиперболы) и слева от прямой х = -а (левая ветвь гиперболы).

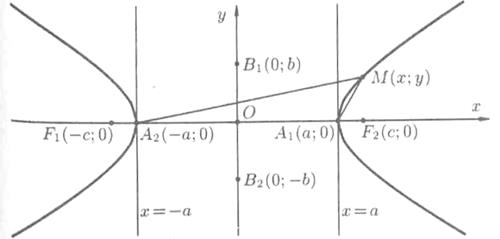
Рис. 7.

4. Из уравнения (11.9) гиперболы видно, что когда |х| возрастает, то и |у| воз­растает. Это следует из того, что разность сохраняет постоянное значение, равное единице.

Из сказанного следует, что гипербола имеет форму, изображенную на рисунке 7 (кривая, состоящая из двух неограниченных ветвей).

Дата добавления: 2015-07-11