Читайте также:
|
Гипербола 
называется равносторонней, если ее полуоси равны (а = b). Ее каноническое уравнение х2-у2=а2.
Асимптоты равносторонней гиперболы имеют уравнения у = х и у = - х и, следовательно, являются биссектрисами координатных углов.
Рис. 10.
Рассмотрим уравнение этой гиперболы в новой системе координат Ох'у' (см. рис. 10), полученной из старой поворотом осей координат на угол 
. Используем формулы поворота осей координат:
х = х' cos α — у' sin α,
у = х' sin α + у' cos α.
Подставляем значения х и у вуравнение:
где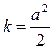 
.
Уравнение равносторонней гиперболы, для которой оси Ох и Оу являются асимптотами, будет иметь вид 
.
Дата добавления: 2015-07-11; просмотров: 139 | Нарушение авторских прав