Читайте также:
|
Эксцентриситетом гиперболы 
называется отношение расстояния между фокусами к величине действительной оси гиперболы, обозначается ε: 
.
Так как для гиперболы с > а, то эксцентриситет гиперболы больше единицы: ε > 1. Эксцентриситет характеризует форму гиперболы. Действительно, из равенства b2 = c2 – a2 следует, что 
, т. е. 
Отсюда видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение - ее полуосей, а значит, тем более вытянут ее основной прямоугольник.
Эксцентриситет равносторонней гиперболы равен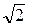 
. Действительно,
Фокальные радиусы 
для точек правой ветви гиперболы имеют вид r1 = εх + а и r2 = εх - а, а для левой – r1 = - (εx + а) и r2 = - (εх - а).
Прямые 
называются директрисами гиперболы. Так как для гиперболы ε > 1, то 
< а. Это значит, что правая директриса расположена между центром и правой вершиной гиперболы, левая — между центром и левой вершиной.
Директрисы гиперболы имеют то же свойство 
= ε, что и директрисы эллипса.
Кривая, определяемая уравнением 
, также есть гипербола, действительная ось 2 b которой расположена на оси Оу, а мнимая ось 2а — на оси Ох. На рисунке 11 она изображена пунктиром.
Очевидно, что гиперболы 
= 1 и имеют общие асимптоты. Такие гиперболы называются сопряженными.
Рис. 11.
4. Парабола
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через р (р > 0).
Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположим посередине между фокусом и директрисой (см. рис. 12). В выбранной системе фокус F имеет координаты 
, а уравнение директрисы имеет вид х = - 
, или х + = 0.
 |
Рис. 12.
Пусть М(х;у) — произвольная точка параболы. Соединим точку М с F. Проведем отрезок MN перпендикулярно директрисе. Согласно определению параболы MF = MN. По формуле расстояния между двумя точками находим:
 |
т. е. у2 = 2рх.
Уравнение у2 = 2рх называется каноническим уравнением параболы.
Парабола есть линия второго порядка.
Дата добавления: 2015-07-11; просмотров: 85 | Нарушение авторских прав