Дополнительные сведения об эллипсе

Форма эллипса зависит от отношения 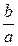. При b = а эллипс превращается в окружность, уравнение эллипса 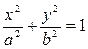принимает вид х²+у² = а². В качестве характеристики формы эллипса чаще пользуются отношением .

Отношение половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой ε («эпсилон»): ε = , причем 0<ε< 1, так как 0 < с < a. С учетом равенства а² - с² = b ² формулу можно переписать в виде

Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс бу­дет менее сплющенным; если положить ε = 0, то эллипс превращается в окружность.

Пусть М(х;у) — произвольная точка эллипса с фокусами F₁ и F₂ (см. рис. 4). Длины отрезков F₁M = r₁ и F₂M = r₂ называются фокальными радиусами точ­ки М. Очевидно, r₁ + r₂ = 2а.

Имеют место формулы r₁ = a + εx и r₂ = a - εx

Прямые называются директрисами эллипса. Значение директрисы эллипса выявляется следующим утверждением:

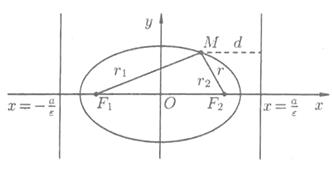
Рис. 4. Рис. 5.

Теорема 1. Если r - расстояние от произвольной точки эллипса до какого-нибудь фокуса, d — расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение 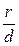есть постоянная величина, равная эксцентриситету эллипса: 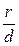= ε.

Из равенства а² - с² = b ² следует, что а > b. Если же а < b, то уравнение 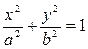определяет эл­липс, большая ось которого 2 b лежит на оси Оу, а малая ось 2а — на оси Ох (см. рис. 5). Фокусы такого эллипса находятся в точках F₁ (0; с) и F ₂(0; -с), где с = .

3. Гипербола

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Обозначим фокусы через F₁ и F₂, расстояние между ними через 2 с, а модуль разности расстоя­ний от каждой точки гиперболы до фокусов через 2а. По определению 2а < 2с, т. е. а < с.

Для вывода уравнения гиперболы выберем си­стему координат Оху так, чтобы фокусы F₁ и F₂ лежали на оси Ох, а начало координат совпало с серединой отрезка F₁F₂ (см. рис. 6). Тогда фокусы будут иметь координаты F₁(-c;0) и F₂(c;0). Пусть М(х; у) — произвольная точка гиперболы. Тогда согласно опре­делению гиперболы | MF₁ - MF₂| = 2а или MF₁ - MF₂ = ±2 а, т.е.

После упрощений, как это было сделано при выводе уравнения эллипса, получим каноническое уравне­ние гиперболы , где b² = c² – a².

Гипербола есть линия второго порядка.

Рис. 6.

---

Дата добавления: 2015-07-11