
|
Читайте также: |
1. Определение параболы и её уравнение
Определение. Параболой называется множество всех точек плоскости, для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой d, не проходящей через данную точку F.
Точка F называется фокусом параболы, а прямая d ─ директрисой параболы. Расстояние от фокуса до директрисы называется фокальным параметром параболы и обозначается: 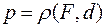 .
.
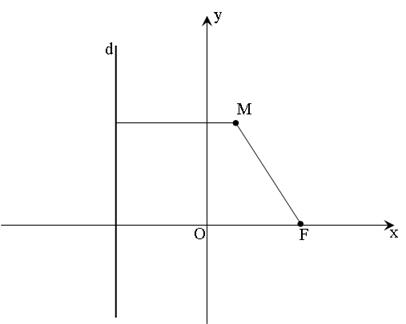
Рис.12.
Для того чтобы составить уравнение параболы на плоскости введём ортонормированную систему координат, ось (Ох) которой выберем проходящей через фокус F параболы перпендикулярно директрисе d. Пусть D─ точка пересечения оси (Ох) с директрисой d. Начало системы координат выберем в точке, являющейся серединой отрезка [FD]. 








 (Рис.12.)
(Рис.12.)
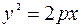 (7) (7)
|
В этом случае фокусы параболы принимает координаты 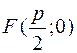 ,а директриса определяется уравнением
,а директриса определяется уравнением 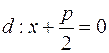 . Пусть М(х;у) ─ произвольная точка параболы. Тогда, по определению,
. Пусть М(х;у) ─ произвольная точка параболы. Тогда, по определению, 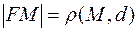 . Учитывая, формулы расстояния между двумя точками и расстояния от точки до прямой, получаем.
. Учитывая, формулы расстояния между двумя точками и расстояния от точки до прямой, получаем. 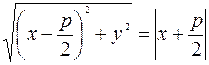 . Возведём это равенство в квадрат.
. Возведём это равенство в квадрат. 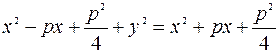 =>
=>
Таим образом, получаем, если точка М(х;у) принадлежит параболе, то её координаты удовлетворяют уравнению.
Покажем теперь, что если координаты некоторой точки М1(х1;у1) удовлетворяют уравнению (7), то точка М1 принадлежит параболе.
И так, пусть для координат точки М1 выполнено условие: 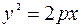 . Вычислим
. Вычислим 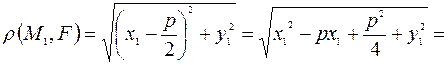
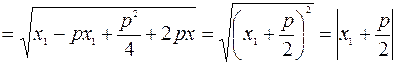 . =>
. => 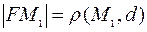 => =>
=> => 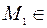 параболе. Таким образом, уравнение (7) является уравнением параболы.
параболе. Таким образом, уравнение (7) является уравнением параболы.
2. Исследование формы параболы по его уравнению
Пусть дана парабола своим каноническим уравнением (7).
Для определения вида кривой заданной уравнением (7), заметим:
а) Координаты начала системы координат точки О(0;0) не удовлетворяют
уравнению (7). => Парабола проходит через начало координат.
б) Если точка М(х;у) принадлежит параболе, то из уравнения (7) следует, что и точка М1(-х;у) принадлежит параболе. => Парабола симметрична относительно оси Ох.
в) 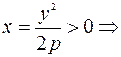 Если
Если 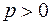 , то все точки параболы расположены в полуплоскости
, то все точки параболы расположены в полуплоскости 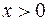 .
.
г) Продифференцируем равенство 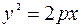 по х:
по х: 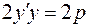 .
. 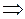
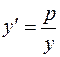 => При у > 0 функция у(х) является возрастающей, а при у < 0 ─ убывающей.
=> При у > 0 функция у(х) является возрастающей, а при у < 0 ─ убывающей.
д) Продифференцировав выражение 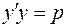 по переменной х, получаем:
по переменной х, получаем: 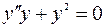 . => Кривая
. => Кривая 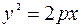 при у > 0 ─ выпукла, а при у < 0─ вогнута.
при у > 0 ─ выпукла, а при у < 0─ вогнута.
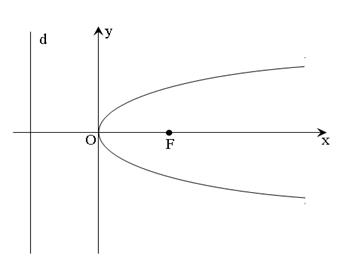
Рис. 13.
Проведённое исследование позволяет построить изображение параболы, приведённое на рис. 13.
3.Построение точек параболы
Построить параболу с фокусом в точке F и директрисой d можно следующим образом.
а) Через фокус F проводим прямую (Ох), перпендикулярную директрисе d.
б) Строим вершину параболы, то есть точку О, которая является серединой отрезка [ON], где N точка пересечения директрисы и (Ох).
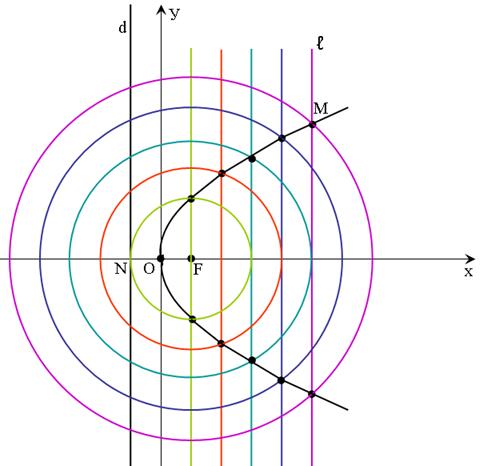
Рис. 14.
в) Проводим произвольную прямую ℓ параллельную директрисе.
г) Строим окружность 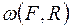 , где
, где 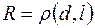 . Точка М= ω∩ℓ принадлежит параболе с фокусом в точке F и директрисой ℓ.
. Точка М= ω∩ℓ принадлежит параболе с фокусом в точке F и директрисой ℓ.
Чтобы получить достаточное число точек параболы необходимо повторить пункты в) и г).
Дата добавления: 2015-07-11; просмотров: 191 | Нарушение авторских прав