|
Читайте также: |
Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух заданных точек 
и 
(фокусов) постоянна и равна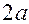 
. Из этого определения после несложных преобразований 
получается каноническое уравнение:
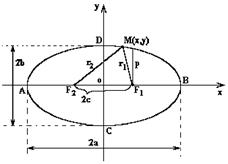
О - центр эллипса
- вершины
и - фокусы;
ОА= 
и ОС= 
- полуоси;
эксцентриситет
Окружность - частный случай эллипса при 
и 
5.2 Гипербола
Гиперболой называется геометрическое место точек плоскости, для которых модуль разности расстояний до двух заданных точек и (фокусов) постоянна и равна 
.
Как и в предыдущем случае, из определения получено каноническое уравнение гиперболы: 
О - центр гиперболы
А и В - вершины
и - фокусы
AB =2 a - действительная ось; CD =2 b - мнимая ось;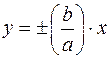 
- асимптоты гиперболы;
, 
- эксцентриситет
При = гипербола – равносторонняя (в середине – квадрат)
__________________________________________________________
Парабола
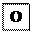
Параболой называется геометрическое место точек, равноудалённых от заданной точки F (фокуса) и от данной прямой (директрисы).
Аналогично из определения получено каноническое уравнение гиперболы y 2 = 2 px
О – вершина; ox - ось параболы точка F – фокус
- уравнение директрисы
- эксцентриситет (все параболы подобны друг другу и зависят только от 
).
§6*. Поверхности второго порядка (обзор)
Общее уравнении поверхности второго порядка:
(2)
С помощью соответствующих переносов и поворотов осей координат можно добиться, чтобы уравнение имело самый простой (канонический) вид. Рассмотрим эти варианты.
6.1 Эллипсоид
. 
- полуоси
При равенстве двух полуосей поверхность называется эллипсоид вращения
При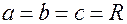 
имеем сферу радиуса 
__________________________________________________________
6.2. Гиперболоиды.
А. Однополостный гиперболоид 
.
При 
получается однополостный гиперболоид вращения.
В. Двуполостный гиперболоид
.
и - полуоси
При получается двуполостный гиперболоид вращения.
__________________________________________________________
Дата добавления: 2015-07-11; просмотров: 126 | Нарушение авторских прав