Эксцентриситет эллипса

Рассмотрим эллипс с фокусами в точках F₁ и F₂ , большой полуосью которого является [A₁A₂].

Определение. Эксцентриситетом эллипса называется число, равное .

Так как , то ε > 0. Для окружности => ε = 0.

Пусть эллипс задан уравнением 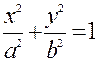, тогда => => => . => Эксцентриситет определяется отношением полуосей эллипса.

Рис.3.

При ε = 0 получаем , что указывает на то, что в этом случае

эллипс является окружностью. При стремлении ε к единице отношение полуосей становится меньше и стремится к нулю. Зафиксируем значение большой полуоси эллипса и пусть ε → 0. Изменение формы эллипса, в этом случае показано на Рис.3.

ВЫВОД. Эксцентриситет характеризует степень вытянутости эллипса вдоль большой оси.

Дата добавления: 2015-07-11