Исследование уравнения гиперболы

1. Гипербола состоит из двух, не связанных друг с другом, частей: первая при , вторая при . Они называются ветвями гиперболы, то есть гипербола лежит вне основного прямоугольника. Точки и – вершины гиперболы.

2. Гипербола симметрична относительно обеих осей координат и начала координат. Начало координат является центром симметрии гиперболы, его тоже называют центром гиперболы.

3. Асимптоты гиперболы.

Определение 3.2 Прямая линия является асимптотой линии , если расстояние от точки линии до прямой стремится к 0 при неограниченном удалении этой точки от начала координат.

Покажем, что существуют прямые, к которым ветви гиперболы приближаются при .

Прямые и являются асимптотами гиперболы.

4. Фокусы гиперболы.

Точки 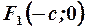и являются фокусами гиперболы, если .

5. Эксцентриситет гиперболы.

Число — называется эксцентриситетом гиперболы. Так как для гиперболы , то .

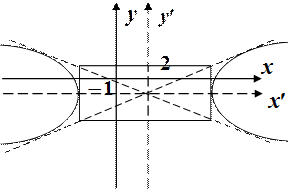
Построение гиперболы

1. Строим основной прямоугольник: прямые . Диагонали этого прямоугольника – прямые, имеющие уравнения

и

то есть - асимптоты гиперболы.

2. Отмечаем вершины гиперболы .

3. Строим гиперболу, учитывая её симметрию относительно осей и начала координат.

Отметим, что в отличии от эллипса, гипербола лежит вне основного прямоугольника.

Если начало координат перенесено в точку 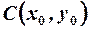– то получим уравнение гиперболы со смещённым центром

(3.2)

Задача. Построить гиперболу

Дата добавления: 2015-07-11