Для второго расчетного случая коэффициент запаса устойчивости определялся по формуле

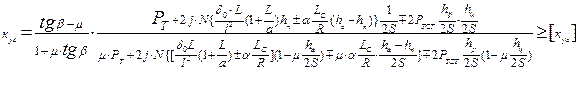
(5)

где Р_Т - вертикальная нагрузка от тележки на путь с учетом ее обезгрузки при эксцентричном действии продольных сил;

Р_ТСТ - вертикальная статическая нагрузка от тележки на путь;

j и a - коэффициенты перекоса;

N - расчетные продольные сжимающие силы, действующие на автосцепки вагона;

2d₀ - суммарный поперечный разбег рамы хоппера относительно оси пути в направляющем сечении (по шкворню);

2l,2L,2Lс - соответственно база вагона, расстояние между упорными плитами автосцепок и длина вагона по осям сцепления автосцепок;

а – длина корпуса автосцепки от оси сцепления до конца хвостовика;

hn, ha, hц, - соответственно высоты рабочей плоскости пятника, оси автосцепки и центра тяжести вагона над уровнем плоскости головок рельсов;

hр – возвышение наружного рельса в кривой;

2S – расстояние между кругами катания колес, 2S =1,6 м;

R – радиус кривой, R =250 м.

Вертикальная нагрузка от тележки на путь с учетом ее обезгрузки под действием продольной силы, вызванной разностью высот осей автосцепок исследуемого и соседнего вагонов, определялась по формуле

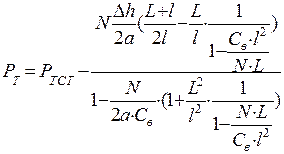, (6)

где Δh – разность уровней осей автосцепок в соединении 2-х вагонов, Δh = 0,08 м;

Св - вертикальная жесткость рессорного подвешивания одной тележки.

Коэффициенты j и a определялись по формулам

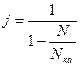, (7)

, (8)

где Nка и Nкб продольные критические силы, приводящие к относительному перекосу вагонов и осей автосцепок в плане, определялись из выражений

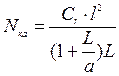, (9)

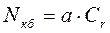, (10)

где Сr – горизонтальная жесткость рессорного подвешивания одной тележки.

Перед определением 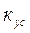проверялось выполнение условия

d_у <[d_у], (11)

где d_у и [d_у ] – соответственно упругая поперечная деформация рессорных комплектов тележек под действием поперечных горизонтальных сил Н, приложенных к пятникам тележек, и предельное (по конструкции) поперечное одностороннее смещение надрессорной балки относительно рамы тележки.

Значение H определялось по формуле

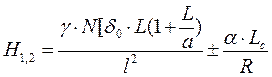, (12)

Результаты расчета для первого расчетного случая (груженый вагон) приведены в таблице 2, порожний вагон в таблице 3.

Таблица 2 - Результаты расчета для первого расчетного случая (груженый вагон)

Наименование	Обозначение	Величина
Средне вероятное значение коэффициента вертикальной динамики		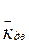0,25
Расчетное значение коэффициента вертикальной динамики		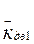0,19
Расчетное значение коэффициента динамики боковой качки		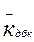0,06
Среднее вероятное значение рамной силы, т		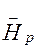2,59
Коэффициент запаса устойчивости		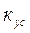2,04

Таблица 3 - Результаты расчета для первого расчетного случая (порожний вагон)

Наименование	Обозначение	Величина
Средне вероятное значение коэффициента вертикальной динамики		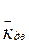0,51
Расчетное значение коэффициента вертикальной динамики		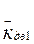0,38
Расчетное значение коэффициента динамики боковой качки		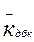0,13
Средне вероятное значение рамной силы, т		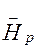1,09
Коэффициент запаса устойчивости		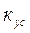1,48

Результаты расчета от выжимания порожнего вагона в кривой при наличии возвышения наружного рельса приведены в таблице 4.

Результаты расчета от выжимания порожнего вагона в кривой при отсутствии возвышения наружного рельса приведены в таблице 5.

Таблица 4 - Расчет коэффициента устойчивости при наличии возвышения наружного рельса

Наименование	Обозначение	Величина
Возвышение наружного рельса, м	hр	0,15
Коэффициент запаса устойчивости, при опрокидывании внутрь кривой		2,63
Коэффициент запаса устойчивости, при опрокидывании наружу кривой		2,68

Таблица 5 - Расчет коэффициента устойчивости при отсутствии возвышения наружного рельса

Наименование	Обозначение	Величина
Коэффициент запаса устойчивости, при опрокидывании внутрь кривой		2,38
Коэффициент запаса устойчивости, при опрокидывании наружу кривой		3,11

Дата добавления: 2015-07-10