Приведение к каноническому виду уравнения центральной кривой

Пусть дано уравнение (1.1), определяющее центральную кривую второго порядка Г.

а) Совершим параллельный перенос начала координат в точку - центр данной кривой.

Определим координаты центра по формулам (1.16).

В новой системе координат уравнение (1.1) будет иметь вид (см. (1.26))

. (1.33)

Коэффициенты уравнения (1.33) связаны с коэффициентами уравнения (1.1) соотношениями (1.25).

б) Если , то дальнейшее упрощение уравнения (1.33) достигается при помощи поворота осей координат на угол 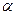, удовлетворяющему условию (1.31). В результате поворота получится уравнение вида

(1.34)

соответствующее одному из канонических уравнений 1), 2), 3), 4), 5) (см. теорему 1). Коэффициенты уравнения (1.34) связаны с коэффициентами уравнения (1.33) соотношениями (1.29).

Дата добавления: 2015-07-11