Классификация поверхностей второго порядка.

Центром поверхности второго порядка S называется такая точка пространства, по отношению к которой точки этой поверхности расположены симметрично парами. Точка 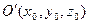является центром поверхности второго порядка, определяемой уравнением (3.1), в том и только том случае, когда ее координаты удовлетворяют уравнениям:

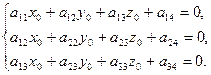(3.17)

Определитель этой системы равен . Если 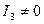, то система имеет единственное решение. В этом случае поверхность будет иметь единственный центр, координаты которого определены формулами:

(3.18)

Такую поверхность второго порядка называют центральной.

Классификация поверхностей второго порядка по группам (теорема 2) совпадает с классификацией поверхности второго порядка по характеру центров (точка, прямая, плоскость, нет центров).

Если система (3.17) несовместна

Дата добавления: 2015-07-11