Гиперболический параболоид

Гиперболический параболоид (рис. 3.9) имеет каноническое уравнение: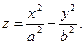

Сечения, параллельные плоскости Oyz – конгруэнтные (одинаковые) параболы; сечения, параллельные плоскости Oxz – также конгруэнтные параболы; сечения, параллельные плоскости Oxy – гиперболы (а также пары пересекающихся прямых).

Гиперболический параболоид (рис. 3.10), имеет два семейства образующих:

I.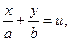

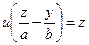
II.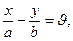

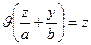
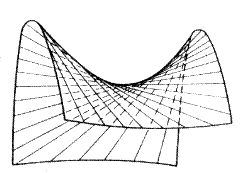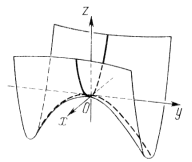
Рис. 3.9. Рис. 3.10.

Здесь u и 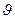- также произвольные величины. Через каждую точку поверхности проходят две прямые: по одной образующей из каждого семейства (на рис. 3.10 показано лишь одно семейство прямых).

7.7. Цилиндры. Параболический цилиндр

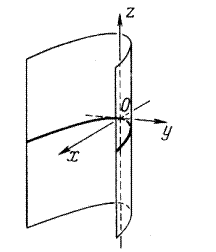
Форма цилиндров определяется их направляющими. Будем считать, что направляющие цилиндров расположены в плоскости Oxy, образующие – параллельны оси Oz.

Тогда, исходя из формы образующей, цилиндры могут быть: эллиптические, гиперболические, параболические.

В качестве примера одного из трех видов цилиндров 2-го порядка приведем параболический цилиндр, который имеет каноническую формулу: .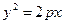

Рис. 3.11.

Дата добавления: 2015-07-11