Приведение общего уравнения кривой второго порядка к каноническому виду

Если кривая Г задана в декартовой прямоугольной системе координат 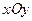уравнением (2.1), то, применяя преобразования поворота осей координат и переноса начала координат можно привести уравнение к каноническому виду.

Преобразование коэффициентов при параллельном переносе

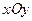Пусть дано уравнение (2.1), определяющее кривую второго порядка Г. Совершаем параллельный поворот начала координат в точку . При этом координаты x, y произвольной точки плоскости М в системе координат и координаты в новой системе координат связаны соотношениями:

(5.1)

Подставляя выражения (1.23) в уравнение (2.1), получим уравнение кривой в новой системе координат

, (5.2)

где

(5.3)

Отметим, что при параллельном переносе начала координат старшие коэффициенты не изменяются, а коэффициенты 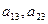и свободный член 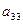преобразуются по формулам (1.25).

Предположим теперь, что уравнение (1.1) определяет центральную кривую второго порядка ().

Совершим параллельный перенос начала координат в точку -центр данной кривой. Так как координаты центра удовлетворяют уравнениям

то в новой системе координат в уравнении (1.24) коэффициенты равны нулю и уравнение примет вид

. (5.4)

Преобразование коэффициентов при повороте

Пусть дано уравнение (1.1), определяющее кривую второго порядка. В случае, когда , выполним преобразование поворота осей координат на угол 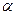. При этом координаты x, y произвольной точки плоскости М в системе координат 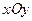и координаты в новой системе координат связаны соотношениями:

(1.27)

Подставляя (1.27) в уравнение кривой (1.1), получим

Приведем это уравнение к виду

(1.28)

Коэффициенты уравнений (1.1) и (1.28) в системах координат 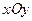и соответственно связаны соотношениями:

(1.29)

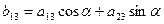
Таким образом, при повороте осей координат на угол 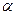коэффициенты преобразуются по формулам (1.29), а свободный член 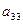не изменяется.

Покажем, что существует угол 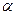такой, что в преобразованном уравнении (1.28) коэффициент при равен нулю. Действительно, согласно второй из формул (1.29) условие эквивалентно равенству

(1.30)

Следовательно, достаточно угол 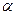выбрать из условия

(1.31)

После поворота на угол 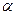, удовлетворяющий условию (1.31), уравнение (1.1) не будет содержать слагаемое с произведением , то есть в новой системе координат исходное уравнение примет вид:

(1.32)

Замечание 1. Корни квадратного уравнения (1.31) соответствует двум взаимно перпендикулярным направлениям (так как по теореме Виета ). Поэтому, выбирая вместо , мы только меняем ролями оси и .

Замечание 2. Значения и выражаются через по формулам

(1.33)

Замечание 3. Угол 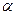можно также выбрать из условия

(1.32)

которое следует из равенства (1.30).

---

Дата добавления: 2015-07-11