|
Читайте также: |
Приведем в качестве примера историческую динамику объема двух потребительских рынков. Несложно отметить, что логистическая кривая действительно может описывать процесс, представленный на рис. 1 и 2 - рост и стабилизация рынка, а во втором – завершение фазы начала выхода на рынок.
Рис.1. Динамика потребления домашнего сыра
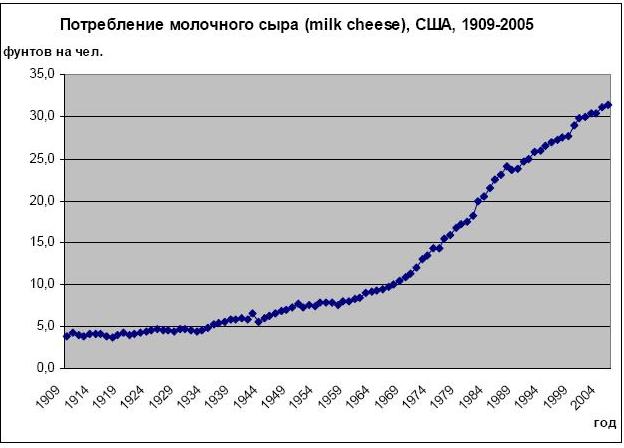
Рис.2. Динамика потребления молочного сыра
В результате параметры модели приобретут следующий экономический смысл:
Q – объём рынка;
t – время;
– рост рынка в единицу времени;
- потенциальный рост рынка;
– геометрический рост.
К – потенциальная (максимальная) ёмкость рынка;
– относительная свободная ниша на рынке (свободные возможности роста);
– логистическая кривая Фергельст - Перля.
– конкурентное сопротивление;
– интенсивность конкурентной борьбы.
Для описания процесса и выявления тенденций развития явлений выполняют построение теоретической S-ой логистической функции. График этой функции имеет форму латинской буквы «S»положенной на бок (образная кривая). Кривая имеет две точки перегиба, которые характеризуют переход от ускорения роста к равномерному движению (вогнутость) и затем к замедлению (выпуклость).
С помощью этой кривой можно определить оптимальные, критические и другие практически ценные точки.
Искомую логистическую функцию описывает уравнение Ферхюльста
(1)
где У(х) значение функции;
х- время;
А – расстояние между верхней и нижней асимптотами,
С – нижняя асимптота, т.е. предел, с которого начинается рост функции.
Параметры а и б, определяют наклон, изгиб, точки перегиба логистической кривой.
| У |
| О |
| А/2 |
| А |
| С |
| Х |
| У |
| О |
| - в |
б)
| Х |
| У |
| О |
| Х |
| + в |
в)
Рис.3. Графики логистических функций
При определении параметров уравнения логистической функции сначала определяют верхнюю и нижнюю асимптоты.
Это можно выполнить двумя способами:
1. Визуальным осмотром эмпирического графика.
2. С использованием зависимости
(2)
где 
- три эмпирических значения функции, взятых через равные интервалы аргумента.
Для определения параметров уравнения (1) используем систему уравнений (3), составленную при помощи метода наименьших квадратов.
(3)
Если С=0, а верхняя асимтота А= 100% или 1, то уравнение логистической функции упрощается до формы
. (4)
С помощью кривой можно описывать долю отдельной компании на рынке. Такой аппарат можно применять для динамичных компаний, обгоняющих рынок. При этом компания должна проводить агрессивную маркетинговую кампанию или обладать компетентными преимуществами, например: сильным менеджментом; интеллектуальными разработками, защищенными патентом; производством нишевого товара, не представленного на рынке, и т.д. С точки зрения корпоративных финансов ценность логистической кривой состоит не столько в описании динамики рынков, сколько в прогнозировании на основе кривой их будущего роста. Первый шаг — решение дифференциального уравнения логистической кривой:
. (5)
Здесь существует два подхода по оценке неизвестных параметров. Во-первых, это эконометрический расчет коэффициентов по историческим данным. Здесь, к сожалению, существует ряд проблем. Необходимо обладать продвинутой техникой эконометрических расчетов, так как модель нелинейная. Более того, по развивающимся рынкам имеется незначительное число исторических данных, в основном сосредоточенных в первой фазе. В результате оценки параметров обладают низкой значимостью.
Альтернативным подходом можно считать формирование параметров на основе их экономического смысла, а именно:
К – потенциальная ёмкость рынка;
– относительный потенциал роста в момент времени t=0;
– средний темп роста в первые годы.
В качестве «потолка роста» можно предложить использовать показатели рынка соответствующего товара в развитых странах, сходных по культурным особенностям и пристрастиям в потреблении. Потребление товара на душу населения должно обладать в эталонных странах относительной стабильностью.
Таким образом, модель логистической кривой может быть успешно применена для описания товарных рынков.
Дата добавления: 2015-07-10; просмотров: 591 | Нарушение авторских прав