
|
Читайте также: |
Гиперболой называется множество точек плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Пусть M - точка гиперболы с фокусами F 1 и F 2. Тогда F1 M- F2M =2 a, где а – const. Если F1F2 =2 с, то 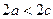 , то есть
, то есть 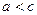 .
.
Выберем систему координат  так, что точка О находится в середине отрезка F1F2 и ось
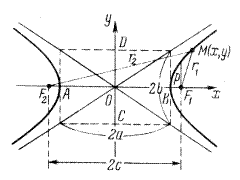
так, что точка О находится в середине отрезка F1F2 и ось  направлена от F1 к F2. Гипербола состоит из двух ветвей и в канонической системе координат имеет вид:
направлена от F1 к F2. Гипербола состоит из двух ветвей и в канонической системе координат имеет вид:
 | |||
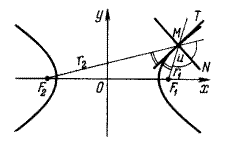 | |||
Рис. 1.3 Рис. 1.4
Вершины А и В гиперболы лежат на действительной оси и 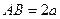 ; на мнимой оси
; на мнимой оси 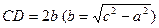 .
.
Каноническое уравнение гиперболы имеет вид:
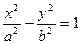 . (1.5)
. (1.5)
Числа а и b называются полуосями гиперболы.
Оси канонической системы координат являются осями симметрии гиперболы, т.к. при замене 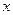 на
на 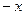 и
и 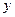 на
на 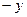 уравнение (2.5) не меняется.
уравнение (2.5) не меняется.
Уравнения асимптот гиперболы (рис. 1.5) имеют вид: 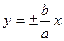 .
.
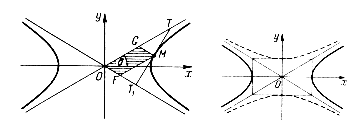 При а = b гиперболу называют равносторонней.
При а = b гиперболу называют равносторонней.
Форма гиперболы характеризуется ее эксцентриситетом 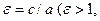 так как
так как 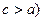 .
.
Рис. 1.5 Рис. 1.6
Расстояния от произвольной точки  гиперболы до ее фокусов F1 и F2 вычисляются по формулам
гиперболы до ее фокусов F1 и F2 вычисляются по формулам
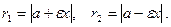
Для правой ветви (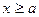 ):
): 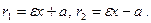
Для левой ветви (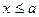 ):
): 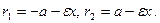
В обоих случаях 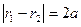 .
.
Директрисы гиперболы имеют уравнения 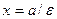 и
и  . Обозначим через d 1 и d2 расстояния от точки M до директрис
. Обозначим через d 1 и d2 расстояния от точки M до директрис 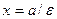 и
и  соответственно. Точка M лежит на гиперболе тогда и только тогда, когда
соответственно. Точка M лежит на гиперболе тогда и только тогда, когда
 ,
,
т.е. отношение расстояния от точки M до фокуса к расстоянию от этой точки до соответствующей директрисы равно эксцентриситету гиперболы.
Уравнение касательной к гиперболе в точке 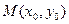 имеет вид
имеет вид
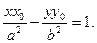
Дата добавления: 2015-07-11; просмотров: 151 | Нарушение авторских прав