Схема приведения кривых 2-го порядка к каноническому виду

1. Вычисляются значения инвариантов для заданного уравнения кривой 2-ого порядка;
2. Уравнение преобразовывается в соответствии с ниже приведенной таблицей:

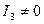
Централные кривые I2 ≠ 0	I2 > 0		Вид кривой	Необходимое преобразование координат	Каноническое уравнение после преобразования
Эллипс: а) -действительный, б) - мнимый ^*	1) Перенос начала в центр кривой, координаты которого x0 и y0: 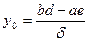2) Поворот осей на угол a, определяемый из: Знак sin(2a) должен совпадать со знаком 2b; угловой коэффициент новой оси Ox':	a’ и c’ являются корнями квадратного уравнения:
	Пара мнимых ^* прямых, имеющих общую действительную точку
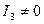
I2 < 0		Гипербола
	Пара пересекающихся прямых
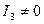
Параболические кривые     ^**		Парабола	1) Перенос начала в вершину параболы, координаты которой x0 и y0 определяются из уравнений: 2) Поворот осей на угол a, определяемый из: Знак sin(a) должен быть противоположен знаку a;
	Пара прямых, параллельных, при d ^2- af >0; сливающихся, при d ^2- af =0; мнимых ^*, при d ^2- af <0;	Поворот осей на угол a, определяемый из: Знак sin(a) должен быть противоположен знаку a;	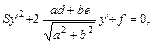приводиться к виду:

^* Может оказаться, что данному общему уравнению не удовлетворяют координаты ни одной действительной точки на плоскости (например, x²+y²+1=0); тогда условно говорят, что данное уравнение изображается мнимой кривой.

^** В случае предполагается, что ни один из коэффициентов a, b, с не равен нулю. Если два коэффициента (а и b или b и c) равны нулю, то упрощение уравнения сводится к параллельному пере­

носу осей; уравнение су² -2 dx +2 ey + f = 0 преобразуется к виду (y-у₀)² = 2p(x-x₀), а уравнение а x²+2 dx +2 ey + f =0- к виду (x-x₀)² = 2p(y-y₀).

Дата добавления: 2015-07-11